The Gas Law Quiz: Chemistry Trivia!

Reviewed by Editorial Team
The ProProfs editorial team is comprised of experienced subject matter experts. They've collectively created over 10,000 quizzes and lessons, serving over 100 million users. Our team includes in-house content moderators and subject matter experts, as well as a global network of rigorously trained contributors. All adhere to our comprehensive editorial guidelines, ensuring the delivery of high-quality content.
Learn about Our Editorial Process
| By Gilvin
G
Gilvin
Community Contributor
Quizzes Created: 3 | Total Attempts: 3,317
| Attempts: 1,306
Quiz Flashcard
SettingsSettings
Please wait...
  • 1/29 Questions

    If the pressure of a gas is 103.2 kPa at a temperature of 100 Celsius and a volume of 4L is changed to a lower pressure of 80 kPa and 100 degrees celsius, what will be the new volume? (Hint: kPa is kilo pascals -- a unit of measure for pressure).

    • 2,064 L
    • 0.3225 L
    • 5.16 L
    • 3.1 L
Please wait...
About This Quiz

Explore the intriguing world of gases with 'The Gas Law Quiz: Chemistry Trivia!' Delve into the behaviors of gases under various conditions, examining concepts like pressure, volume, collisions, and mole calculations. This quiz is perfect for enhancing understanding of fundamental gas laws and their practical applications.

The Gas Law Quiz: Chemistry Trivia! - Quiz

Quiz Preview

  • 2. 

    A gas at a temperature of 80Celsius and a volume of 3.2 Liters is brought into an area with a temperature of 100 Celsius, what is the new volume if the pressure remains constant? Hint 1: This is Charles law (V1/T1 = V2/T2) Hint 2: ALL GAS PROBLEMS MUST use the KELVIN temperature scale. (To change from Celsius to Kelvin: add 273)

    • 3.38 L

    • 2.84 L

    • 3.75 L

    • 2.4 L

    Correct Answer
    A. 3.38 L
    Explanation
    (3L)/(353K) = V2/(373K)
    Math: 3 x 373 divided by 353.

    Rate this question:

  • 3. 

    If the pressure of a gas is 1.2 atmospheres with a volume of 12 L, how much pressure is exerted by the gas if the volume is changed to 9L? (Assume constant temperature)

    • .9 L

    • 129.6 L

    • 6.0 L

    • 1.6 L

    Correct Answer
    A. 1.6 L
    Explanation
    If the variables are only Pressure and Volume, (with constant temperature), this indicates Boyle's Law: P1V1 = P2 V2 (Where 1 indicates the first set of conditions and 2 indicates the second set of conditions). (1.2 atm) (12L) = (P2) (9L) Math: 1.2 times 12 divided by 9.

    Rate this question:

  • 4. 

    What is the volume of  2 moles of Helium at a temperature of 32 degrees Celsius and a pressure of 1.1 atmospheres? Given R = 0.08321 Latm/molK  and 8.314 kPa L/mol K Hint: There is only 1 set of conditions for this gas problem and the moles of the gas is given. This indicates the ideal gas law: PV = nRT.  Remember that n  is equal to the number of moles. P is the pressure, V is the volume and T is the temperature (change to Kelvin). The R MUST match the units in the rest of the problem.  IF pressure is given in atmosphere, then use R = 0.08321 Latm/molK . IF pressure was given in kPa, then use 8.314 Kpa L/mol K Note also that volume MUST be in Liters and Temperature (as for all gas problems) must be in Kelvin.

    • 13.96 L

    • .45 L

    • 46.14 L

    • 4,610 L

    Correct Answer
    A. 46.14 L
    Explanation
    (1.1 atm) (V) = (2 moles) (0.08321 L atm/molK) (305K)

    Rate this question:

  • 5. 

    What is the temperature of  3.4 moles of Helium at a  pressure of 1.1 atmospheres and a volume of 3.7 Liters? (What is the temperature in Kelvin?) Given R = 0.08321 Latm/molK  and 8.314 kPa L/mol K

    • 14.39 K

    • 12.15 K

    • 0.1 K

    • 142 K

    Correct Answer
    A. 14.39 K
    Explanation
    (1.1 atm) (3.7 L) = (3.4 moles) (0.08321 Latm/mol K) (T)

    Rate this question:

  • 6. 

    A 180.0 mL volume of gas is measured at 87ºC.  If the pressure remains unchanged, what is the volume of the gas at standard temperature?

    • 0.0 mL

    • 0.5 mL

    • 137 mL

    • 410 mL

    Correct Answer
    A. 137 mL
    Explanation
    When the pressure of a gas remains constant, its volume is directly proportional to its temperature. This relationship is described by Charles's Law. According to Charles's Law, as the temperature of a gas decreases, its volume also decreases. Standard temperature is defined as 0°C or 273 K. Since the given gas is initially measured at 87°C, which is higher than the standard temperature, the volume of the gas will decrease when it is brought to standard temperature. Therefore, the correct answer is 137 mL, which is the only option that represents a decrease in volume from the initial 180.0 mL.

    Rate this question:

  • 7. 
    A gas in a balloon measures 2.2 L, 1.1 atmospheres, and 32 degrees Celsius. The environment is changed and the balloon is now 1.8 L and 1.4 atmospheres. What is the new temperature? Hint 1: Always change the temperature to the Kelvin scale. Hint 2: Pressure, volume, and temperature are all changed. Use the combined gas law: - ProProfs

    A gas in a balloon measures 2.2 L, 1.1 atmospheres, and 32 degrees Celsius. The environment is changed and the balloon is now 1.8 L and 1.4 atmospheres. What is the new temperature? Hint 1: Always change the temperature to the Kelvin scale. Hint 2: Pressure, volume, and temperature are all changed. Use the combined gas law:

    • 317.6 K

    • 33.32 K

    • 384.3 K

    • 0.02 K

    Correct Answer
    A. 317.6 K
    Explanation
    The new temperature can be calculated using the combined gas law, which states that the product of pressure and volume divided by temperature remains constant. By rearranging the equation and plugging in the given values, we can solve for the new temperature. In this case, the new temperature is calculated to be 317.6 K.

    Rate this question:

  • 8. 

    What pressure (atm) is exerted by .750 mol of a gas at a temperature of 273 K and a volume of 5.00 L?

    • 2.1 atm

    • 3.4 atm

    • 4.98 atm

    • 760 atm

    Correct Answer
    A. 3.4 atm
    Explanation
    The pressure exerted by a gas can be calculated using the ideal gas law equation, which states that pressure is equal to the number of moles of gas multiplied by the gas constant, multiplied by the temperature in Kelvin, divided by the volume. In this case, we are given the number of moles of gas (.750 mol), the temperature (273 K), and the volume (5.00 L). Plugging these values into the equation, we can calculate the pressure exerted by the gas, which is 3.4 atm.

    Rate this question:

  • 9. 

    A gas in a balloon measures 3.6 L, 0.9 atmospheres, and 34 degrees Celsius. The environment is changed and the balloon is now 1.4 atmospheres at a temperature of 38 degrees Celsius. What is the new volume?

    • 2.59 L

    • 4.6 L

    • 220,961 L

    • 2.34 L

    Correct Answer
    A. 2.34 L
    Explanation
    The ideal gas law states that the product of pressure and volume is directly proportional to the product of the number of moles of gas and the temperature in Kelvin. Therefore, we can use the equation P1V1/T1 = P2V2/T2 to solve for the new volume. Plugging in the given values, we have (0.9 atm)(3.6 L)/(34 + 273) K = (1.4 atm)(V2)/(38 + 273) K. Solving for V2 gives us V2 = (0.9 atm)(3.6 L)(38 + 273) K / (34 + 273) K / (1.4 atm) = 2.34 L.

    Rate this question:

  • 10. 

    How many moles are present in a container that is 79.9 Liters with a pressure of 105 kPa and a temperature of 24 degrees Celsius? Given R = 0.08321 Latm/molK  and 8.314 kPa L/mol K

    • 2.7 moles

    • 271 moles

    • 3.4 moles

    • 5.6 moles

    Correct Answer
    A. 3.4 moles
    Explanation
    There is only 1 set of conditions and you are solving for moles, therefore use the ideal gas law: PV = nRT. Since Pressure is given in kPa, you must use R = 8.314 kPa L/mol K. Make sure to change to Kelvin for temperature. (105 kPa) (79.9L) = n (8.314 kPa L/mol K) (297K)

    Rate this question:

  • 11. 

    Why would the pressure of a sample of gas at a constant volume fall 75 mmHg?

    • The container exploded

    • The temperature increased

    • The temperature decreased

    • Fewer particles were present

    Correct Answer
    A. The temperature decreased
    Explanation
    When the temperature of a gas decreases, the average kinetic energy of its particles decreases as well. This causes the particles to move slower and collide with the container walls less frequently and with less force. As a result, the pressure exerted by the gas decreases. Therefore, a decrease in temperature would cause the pressure of a sample of gas at a constant volume to fall.

    Rate this question:

  • 12. 

    A sample of oxygen occupies 560. mL when the pressure is 800.00 mmHg.  At constant temperature, what volume does the gas occupy when the pressure decreases to 700.0 mmHg?

    • 80.0 mL

    • 490. mL

    • 600. mL

    • 640. mL

    Correct Answer
    A. 640. mL
    Explanation
    When the pressure of a gas decreases at constant temperature, the volume of the gas increases. This relationship is described by Boyle's Law, which states that the pressure and volume of a gas are inversely proportional. In this case, the initial volume is 560. mL and the initial pressure is 800.00 mmHg. When the pressure decreases to 700.0 mmHg, the volume of the gas can be calculated using the equation P1V1 = P2V2, where P1 and V1 are the initial pressure and volume, and P2 and V2 are the final pressure and volume. Solving for V2 gives a volume of 640. mL.

    Rate this question:

  • 13. 

    If the temperature of a fixed quantity of gas decreases and the pressure remains unchanged, 

    • Its volume increases

    • Its volume decreases

    • Its volume is unchanged

    Correct Answer
    A. Its volume decreases
    Explanation
    When the temperature of a fixed quantity of gas decreases while the pressure remains unchanged, the volume of the gas decreases. This is because according to the ideal gas law, when the temperature decreases, the average kinetic energy of the gas molecules decreases. As a result, the gas molecules move slower and collide with each other less frequently, leading to a decrease in volume.

    Rate this question:

  • 14. 

    If two moving steel balls collide, their total energy after the collision is the same as before.  This is an example of

    • Boyle's law

    • The law of gravity

    • An elastic collision

    • Both Boyle's and Charles's law.

    Correct Answer
    A. An elastic collision
    Explanation
    An elastic collision is a type of collision where the total kinetic energy of the system is conserved. In this scenario, the two moving steel balls collide, and their total energy after the collision remains the same as before. This indicates that the collision is elastic, as the kinetic energy is not lost or converted into other forms of energy. Therefore, the correct answer is an elastic collision.

    Rate this question:

  • 15. 

    A gas at a temperature of 34 Celsius and a volume of 6.3  Liters is brought into a new area where the gas expands to a volume of 8.0 Liters. What is the new temperature? (Assume constant Pressure)

    • 43.17 K

    • 389.84 K

    • 0.164 K

    • 1.48 K

    Correct Answer
    A. 389.84 K
    Explanation
    This problem uses Charles' law. (V1/T1 = V2/T2)
    MAKE SURE YOU CHANGE YOUR TEMPERATURE TO KELVIN (add 273)!!
    (6.3L)/307K = (8L)/T2
    Math: 8 x 307 divided by 6.3

    Rate this question:

  • 16. 

    A sample of gas at 25ºC has a volume of 11 L and exerts a pressure of 660 mmHg.  How many moles of the gas are in the sample?

    • .39 mol

    • 3.9 mol

    • 9.3 mol

    • 87 mol

    Correct Answer
    A. .39 mol
    Explanation
    The ideal gas law equation, PV = nRT, can be used to solve this problem. We are given the volume (V = 11 L), the pressure (P = 660 mmHg), and the temperature (T = 25°C). We need to find the number of moles (n) of the gas in the sample. Rearranging the equation, we have n = PV / RT. Plugging in the values, we get n = (660 mmHg * 11 L) / (0.0821 L•atm/mol•K * 298 K). After performing the calculation, we find that n is approximately equal to 0.39 mol.

    Rate this question:

  • 17. 

    Which is an example of gas diffusion?

    • Inflating a flat tire

    • The odor of perfume spreading throughout a room

    • A cylinder of oxygen stored under high pressure

    • All of the above

    Correct Answer
    A. The odor of perfume spreading throughout a room
    Explanation
    Gas diffusion refers to the process by which gas molecules move from an area of high concentration to an area of low concentration. In the given options, the odor of perfume spreading throughout a room is the best example of gas diffusion. When perfume is sprayed in one area, the gas molecules of the perfume spread out and move throughout the room, gradually filling the entire space. This is a result of gas diffusion, as the perfume molecules move from an area of high concentration (where it was sprayed) to an area of low concentration (the rest of the room).

    Rate this question:

  • 18. 

    A gas sample with a mass of .467 g is collected at 20ºC amd 732.5 mmHg.  The volume is 200. mL.  What is the molar mass of the gas?

    • 58 g/mol

    • 180 g/mol

    • 290 g/mol

    • 730 g/mol

    Correct Answer
    A. 58 g/mol
    Explanation
    The molar mass of a gas can be calculated using the ideal gas law equation PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the ideal gas constant, and T is the temperature. In this case, the pressure is given as 732.5 mmHg, the volume is given as 200 mL, and the temperature is given as 20°C. We can convert the pressure to atm by dividing by 760 mmHg/atm, and the volume to liters by dividing by 1000 mL/L. Rearranging the equation to solve for n, we have n = (PV) / (RT). Plugging in the given values and the ideal gas constant (0.0821 L·atm/mol·K), we can calculate the number of moles. Finally, we can calculate the molar mass by dividing the mass of the gas sample (0.467 g) by the number of moles. The result is approximately 58 g/mol.

    Rate this question:

  • 19. 

    Which law compares gases at two different sets of conditions, with temperature as a constant and pressure and volume as variables?

    • Charle's Law

    • Boyle's Law

    • Combined Gas Law

    • Ideal gas law

    Correct Answer
    A. Boyle's Law
    Explanation
    Boyle's law: P1V1 = P2V2 Temperature is constant.
    (Where 1 indicates the first set of conditions and a 2 indicates the second set of conditions.
    {Charle's law is V1/T1 = V2/T2 with pressure constant;
    Ideal is PV = nRT and
    combined is PV/T = PV/T}

    Rate this question:

  • 20. 

    The pressure is the force per unit.

    • Volume

    • Area

    • Length

    • Depth

    Correct Answer
    A. Area
    Explanation
    The pressure is defined as the force exerted per unit area. This means that the pressure is calculated by dividing the force applied on an object by the area over which the force is distributed. Therefore, the correct answer is "area" because pressure is the force per unit area.

    Rate this question:

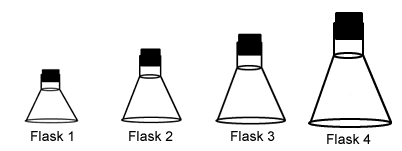
  • 21. 
    Each of these flasks contains the same number of molecules. In which container is the pressure highest? - ProProfs

    Each of these flasks contains the same number of molecules. In which container is the pressure highest?

    • Flask 1

    • Flask 2

    • Flask 3

    • Flask 4

    • Flask 5

    Correct Answer
    A. Flask 1
    Explanation
    As the volume decrease the pressure increases because there are more collisions per unit of surface area within the container.

    Rate this question:

  • 22. 

    Not all Gas Law problems have Kelvin (K) as the unit of temperature. They can be expressed in Celsius (°C)and Fahrenheit(°F). So convert 123°C to K.

    • 396K

    • 486K

    • 369K

    • 458K

    • 693K

    Correct Answer
    A. 396K
    Explanation
    Gas Law problems can be solved using different units of temperature, including Celsius and Fahrenheit. In this case, the question asks to convert 123°C to Kelvin. To convert Celsius to Kelvin, we add 273.15 to the given temperature. Therefore, 123°C + 273.15 = 396.15K. Rounding to the nearest whole number, the correct answer is 396K.

    Rate this question:

  • 23. 

    In a nitrogen gas occupies has a volume of 500ml at a pressure of 0.971atm.What volume will the gas occupy at a pressure of 1.50 atm, assuming the temperature remains constant?

    • 342mL

    • 424mL

    • 324mL

    • 442mL

    • 242mL

    Correct Answer
    A. 324mL
    Explanation
    According to Boyle's Law, at constant temperature, the volume of a gas is inversely proportional to its pressure. This means that as the pressure increases, the volume decreases, and vice versa. In this case, the initial volume of the nitrogen gas is 500 mL at a pressure of 0.971 atm. If the pressure increases to 1.50 atm, the volume of the gas will decrease. The answer of 324 mL indicates that the gas will occupy a smaller volume at the higher pressure.

    Rate this question:

  • 24. 

    By which process do gases take the shape of their container?

    • Evaporation

    • Expansion

    • Adhesion

    • Diffusion

    Correct Answer
    A. Diffusion
    Explanation
    Diffusion is the process by which gases spread out and fill the space available to them. When a gas is placed in a container, its particles move randomly and collide with each other and the walls of the container. As a result of these collisions, the gas particles spread out and occupy the entire space within the container, taking the shape of the container. This process allows gases to evenly distribute themselves and fill any container they are placed in.

    Rate this question:

  • 25. 

    At a pressure of 5.0 atmospheres, a sample of gas occupies 40. liters. What volume will the same sample occupy at 1.0 atmosphere?

    • 0.0050 L

    • 0.13 L

    • 200 L

    • 8.0 L

    Correct Answer
    A. 200 L
    Explanation
    According to Boyle's law, the volume of a gas is inversely proportional to its pressure, assuming constant temperature. Therefore, if the pressure is reduced from 5.0 atmospheres to 1.0 atmosphere, the volume of the gas will increase by a factor of 5. So, the volume of the same sample of gas at 1.0 atmosphere will be 200 L.

    Rate this question:

  • 26. 

    Gas pressure is caused by

    • Gas molecules heating up

    • Gas molecules reacting with other gas molecules

    • Gas molecules hitting the walls of a container

    • Gas molecules hitting other gas molecules

    Correct Answer
    A. Gas molecules hitting the walls of a container
    Explanation
    Gas pressure is caused by gas molecules hitting the walls of a container. When gas molecules move around randomly, they collide with the walls of the container, exerting a force on them. This force per unit area is what we call gas pressure. The more frequent and energetic the collisions, the higher the gas pressure. Heating up the gas molecules or their reactions with other gas molecules may increase their speed and thus the frequency and force of collisions, but ultimately it is the collisions with the container walls that cause gas pressure.

    Rate this question:

  • 27. 

    As the volume of confined gad decreases at a constant temperature, the pressure exerted by the gas ______

    • Decreases

    • Increases

    • Stay the same

    • Fluctuates

    Correct Answer
    A. Increases
    Explanation
    As the volume of confined gas decreases at a constant temperature, the pressure exerted by the gas increases. This is because as the volume decreases, the same amount of gas particles are now confined to a smaller space, leading to more frequent collisions between the particles and the walls of the container. These increased collisions result in a higher pressure being exerted by the gas.

    Rate this question:

  • 28. 

    1.    A sample of argon has a volume of 0.43 mL at 299K. At what temperature in degrees Celsius will it have a volume of 1 mL.

    • 695°C

    • 422°C

    • 428°C

    • 694°C

    Correct Answer
    A. 422°C
    Explanation
    The volume of a gas is directly proportional to its temperature, according to the ideal gas law. This means that as the temperature increases, the volume of the gas also increases. In this question, the initial volume of argon is given as 0.43 mL at 299K, and we are asked to find the temperature at which the volume becomes 1 mL. Since the volume is increasing, we can conclude that the temperature must also increase. Among the given options, the temperature of 422°C is the closest to the initial temperature of 299K. Therefore, the correct answer is 422°C.

    Rate this question:

  • 29. 

    According to Charles Law, if you have a balloon inside a car at noon  during a hot summer day the balloon molecules inside will increase in pressure.

    • True

    • False

    Correct Answer
    A. False
    Explanation
    According to Charles Law Pressure is Constant.

    Rate this question:

Quiz Review Timeline (Updated): Mar 21, 2023 +

Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.

  • Current Version
  • Mar 21, 2023
    Quiz Edited by
    ProProfs Editorial Team
  • Mar 09, 2015
    Quiz Created by
    Gilvin
Back to Top Back to top
Advertisement
×

Wait!
Here's an interesting quiz for you.

We have other quizzes matching your interest.