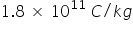Quantum Quiz March 21

Reviewed by Editorial Team
The ProProfs editorial team is comprised of experienced subject matter experts. They've collectively created over 10,000 quizzes and lessons, serving over 100 million users. Our team includes in-house content moderators and subject matter experts, as well as a global network of rigorously trained contributors. All adhere to our comprehensive editorial guidelines, ensuring the delivery of high-quality content.
Learn about Our Editorial Process
| By Saptarshi Ghosh
S
Saptarshi Ghosh
Community Contributor
Quizzes Created: 2 | Total Attempts: 4,940
| Attempts: 851
Quiz Flashcard
SettingsSettings
Please wait...
  • 1/41 Questions

    If one measures the energy of a photon accurately the uncertainty in the measurement of frequency becomes

    • Zero
    • ∞
    • 1
    • ½
Please wait...
About This Quiz

Explore the fundamentals of quantum mechanics with the 'Quantum Quiz March 21'. This quiz covers key topics like the Compton shift, electron diffraction, and blackbody radiation, assessing your understanding of complex physical phenomena and their mathematical descriptions.

Quantum Quiz March 21 - Quiz

Quiz Preview

  • 2. 

    Heisenberg’s Uncertainty Principle states:

    • The more precise a particle's energy can be measured, the less precise its position can be measured

    • The more precise a particle's momentum can be measured, the less precise its position can be measured

    • The more precise a particle's momentum can be measured, the less precise its time can be measured

    • A particle's momentum can be measured exactly

    Correct Answer
    A. The more precise a particle's momentum can be measured, the less precise its position can be measured
    Explanation
    The answer is "The more precise a particle's momentum can be measured, the less precise its position can be measured" because Heisenberg's Uncertainty Principle states that there is a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position and momentum, can be known simultaneously. This means that the more accurately we try to measure the momentum of a particle, the less accurately we can determine its position, and vice versa.

    Rate this question:

  • 3. 

    The number of oscillation modes per unit volume for em standing waves of frequency ν in a blackbody cavity is proportional to

    • ν³

    • ν²

    • ν

    • Hν/(exp[hν/kT] - 1)

    Correct Answer
    A. ν²
    Explanation
    The number of oscillation modes per unit volume for electromagnetic standing waves in a blackbody cavity is determined by the frequency of the waves. As the frequency increases, the number of oscillation modes also increases. The relationship between the number of oscillation modes and the frequency is proportional to ν². This means that as the frequency of the waves increases, the number of oscillation modes per unit volume increases at a faster rate.

    Rate this question:

  • 4. 

    The Compton shift Δλ is twice the Compton wavelength if the scattering angle is

    • 90°

    • 180°

    • 45°

    • 0°

    Correct Answer
    A. 180°
    Explanation
    The Compton shift Δλ is twice the Compton wavelength if the scattering angle is 180°. This is because the Compton shift is the change in wavelength of a photon after it scatters off an electron. When the scattering angle is 180°, it means that the photon is scattered directly back in the opposite direction. In this case, the change in wavelength is maximized and is equal to twice the Compton wavelength, which is a fundamental constant in quantum mechanics.

    Rate this question:

  • 5. 

    The Davisson-Germer experiment demonstrates

    • Electroluminescence

    • Thermionic emission

    • Electron diffraction

    • X-ray diffraction

    Correct Answer
    A. Electron diffraction
    Explanation
    The Davisson-Germer experiment is a famous experiment in physics that demonstrated the wave-particle duality of electrons. In this experiment, a beam of electrons was directed at a crystalline target, and a diffraction pattern was observed on a screen behind the target. This diffraction pattern is similar to the diffraction patterns observed with light waves, confirming that electrons can also behave as waves. Therefore, the correct answer is electron diffraction.

    Rate this question:

  • 6. 

    In Compton scattering, the maximum transfer of energy to the recoil electron happens when the angle of scattering of photons is

    • 90°

    • 180°

    • 135°

    • 60°

    Correct Answer
    A. 180°
    Explanation
    In Compton scattering, the maximum transfer of energy to the recoil electron occurs when the angle of scattering of photons is 180°. This is because at this angle, the photon transfers all of its energy to the electron, resulting in the largest possible energy transfer. At other angles, some of the photon's energy is retained, leading to a smaller transfer of energy to the electron.

    Rate this question:

  • 7. 

    The disagreement between Rayleigh-Jeans' predictions and experimental results for blackbody radiation spectrum is known as

    • Infrared signature

    • Twin paradox

    • Ultraviolet catastrophe

    • Gibb's paradox

    Correct Answer
    A. Ultraviolet catastrophe
    Explanation
    The disagreement between Rayleigh-Jeans' predictions and experimental results for blackbody radiation spectrum is known as the "Ultraviolet catastrophe." This term refers to the failure of classical physics to accurately describe the distribution of energy at high frequencies in the spectrum. According to Rayleigh-Jeans' law, the energy emitted by a blackbody should increase indefinitely as the frequency increases, leading to an infinite energy prediction. However, experimental observations showed that the energy distribution deviated from this prediction, leading to the recognition of this discrepancy as the "Ultraviolet catastrophe."

    Rate this question:

  • 8. 

    The rest mass of a photon of frequency ν is

    • Hν/c

    • Hν/c²

    • Zero

    • Hν²/c

    Correct Answer
    A. Zero
    Explanation
    The rest mass of a photon is zero. According to the theory of relativity, mass and energy are interchangeable, and photons are particles of pure energy. They have no rest mass because they always travel at the speed of light, c. The equation E=mc² shows that an object with rest mass would require an infinite amount of energy to reach the speed of light. Therefore, photons, which travel at the speed of light, have zero rest mass.

    Rate this question:

  • 9. 

    For cavity radiation of wavelength λ at absolute temperature T, Wien's radiation law corresponds to Planck's law when

    • Photon's energy

    • Photon's energy >> kT

    • Photon's energy = kT

    • Photon's energy has any finite value

    Correct Answer
    A. Photon's energy >> kT
    Explanation
    Wien's radiation law corresponds to Planck's law when the photon's energy is much greater than kT. This means that the energy of the photons is significantly larger than the thermal energy of the system, indicating that the radiation is in the high-energy limit. In this regime, the distribution of photon energies follows Planck's law, which describes the spectral energy density of black-body radiation at a given temperature.

    Rate this question:

  • 10. 

    According to Planck, the average energy of cavity oscillators in the frequency range ν to ν+dν is given by

    • Hν/(exp[hν/kT] - 1)

    • Hν/(exp[hν/kT] + 1)

    • Hν

    • Hν.exp[-hν/kT]

    Correct Answer
    A. Hν/(exp[hν/kT] - 1)
    Explanation
    The given formula hν/(exp[hν/kT] - 1) represents the average energy of cavity oscillators in the frequency range ν to ν+dν, according to Planck's theory. This formula takes into account the energy of the oscillators at a given frequency ν, as well as the temperature T. The denominator, exp[hν/kT] - 1, accounts for the distribution of energy levels among the oscillators, which is influenced by the temperature. This formula accurately describes the average energy of the oscillators in the given frequency range according to Planck's theory.

    Rate this question:

  • 11. 

    If visible light is used in Compton scattering the Compton shift will be

    • Negative

    • Zero

    • More positive than what is observed with X-rays

    • Positive but not detectable in the visible window

    Correct Answer
    A. Positive but not detectable in the visible window
    Explanation
    In Compton scattering, the Compton shift refers to the change in wavelength of a photon after it interacts with an electron. This shift is directly proportional to the energy of the incident photon and inversely proportional to the mass of the electron. Since visible light has lower energy compared to X-rays, the Compton shift observed with visible light will be positive but not detectable in the visible window. This means that there will be a slight increase in the wavelength of the scattered photon, but it will not be noticeable within the visible spectrum.

    Rate this question:

  • 12. 

    In Davisson-Germer's experiment the highest peak was obtained at an angle θ = 50° with a voltage of 54 V. The de Broglie wavelength of electrons was

    • 1.67 Å

    • 0.167 Å

    • 0.227 Å

    • 2.27 Å

    Correct Answer
    A. 1.67 Å
    Explanation
    In Davisson-Germer's experiment, the highest peak was obtained at an angle of 50° with a voltage of 54 V. This indicates that the electrons were diffracted by a crystal lattice. The diffraction pattern can be explained by the wave-like nature of electrons, which have a de Broglie wavelength. The de Broglie wavelength is given by the equation λ = h/p, where λ is the wavelength, h is Planck's constant, and p is the momentum of the particle. By rearranging the equation, we can calculate the de Broglie wavelength of the electrons using the given voltage and angle. The correct answer of 1.67 Å indicates the de Broglie wavelength of the electrons in this experiment.

    Rate this question:

  • 13. 

    The peak wavelengths of radiation of a red-hot and a yellow-hot object are 630 nm and 570 nm respectively. If the red-hot object's temperature is 5000 K, the other's temperature is

    • 4000 K

    • 4500 K

    • 5000 K

    • 5500 K

    Correct Answer
    A. 4500 K
    Explanation
    The peak wavelength of radiation is inversely proportional to the temperature of an object according to Wien's displacement law. As the red-hot object has a peak wavelength of 630 nm, which is longer than the peak wavelength of the yellow-hot object (570 nm), it indicates that the red-hot object has a lower temperature. Therefore, the temperature of the yellow-hot object must be higher than 5000 K but lower than 5500 K. The only option within this range is 4500 K, making it the correct answer.

    Rate this question:

  • 14. 

    In Compton scattering, if the angle of scattering varies from 0º to 180º, the electron's recoil angle varies from

    • 0º to 90º

    • 90º to 180º

    • 0º to 180º

    • 0º to 45º

    Correct Answer
    A. 0º to 90º
    Explanation
    In Compton scattering, when the angle of scattering varies from 0º to 180º, the electron's recoil angle varies from 0º to 90º. This means that the electron can recoil at any angle between 0º and 90º relative to the direction of the incident photon. As the angle of scattering increases, the recoil angle of the electron also increases, but it never exceeds 90º. Therefore, the correct answer is 0º to 90º.

    Rate this question:

  • 15. 

    The de Broglie wavelength of a thermal neutron of mass m at temperature T is given by λ =

    • H/√(3mkT)

    • H/√(2mkT)

    • √3h/(mkT)

    • 3h/√(2mkT)

    Correct Answer
    A. H/√(3mkT)
    Explanation
    The de Broglie wavelength of a particle is given by λ = h/p, where h is the Planck's constant and p is the momentum of the particle. In this case, the momentum of the thermal neutron can be related to its kinetic energy using the equation p = √(2mE), where m is the mass of the neutron and E is its kinetic energy. At temperature T, the average kinetic energy of a particle is given by E = (3/2)kT, where k is the Boltzmann constant. Substituting these values into the equation for λ, we get λ = h/√(3mkT).

    Rate this question:

  • 16. 

    The velocities of two particles A and B are 0.05 and 0.02 m sˉ¹ respectively. The mass of B is five times of mass of A. The ratio of their de Broglie’s wavelength is:

    • 1:1

    • 1:4

    • 2:1

    • 4:1

    Correct Answer
    A. 2:1
    Explanation
    The de Broglie wavelength of a particle is inversely proportional to its velocity. Since the velocity of particle A is higher than that of particle B, the de Broglie wavelength of particle A will be smaller than that of particle B. The ratio of their de Broglie wavelengths will be the inverse of their velocities, which is 0.02/0.05 = 2/1. Therefore, the correct answer is 2:1.

    Rate this question:

  • 17. 

    The radiated intensity per unit time from a cavity kept at temperature 1000 Kelvin is 5.67x10ⁿ W/m². The value of n is

    • 8

    • 6

    • 4

    • 12

    Correct Answer
    A. 4
    Explanation
    The radiated intensity per unit time from a cavity is given by the Stefan-Boltzmann law, which states that the radiated intensity is proportional to the fourth power of the temperature. In this case, the temperature is 1000 Kelvin, so the value of n must be 4 in order for the equation to hold true.

    Rate this question:

  • 18. 

    In relation to Rayleigh-Jeans law, the ultraviolet catastrophe refers to the prediction

    • E(ν) → 0 as ν → 0

    • E(T) → ∞ as T → 0

    • E(λ) → ∞ as λ → 0

    • E(λ) → ∞ as λ → ∞

    Correct Answer
    A. E(λ) → ∞ as λ → 0
    Explanation
    The ultraviolet catastrophe refers to the prediction that the energy emitted by a blackbody radiator increases infinitely as the wavelength approaches zero. This prediction is based on the Rayleigh-Jeans law, which describes the energy distribution of blackbody radiation at different wavelengths. According to this law, the energy emitted by a blackbody is proportional to the wavelength to the power of four. As the wavelength approaches zero, the energy emitted becomes infinitely large, leading to the ultraviolet catastrophe.

    Rate this question:

  • 19. 

    The Compton wavelength for electron is

    • 0.24 Å

    • 0.024 Å

    • 2.4 Å

    • 0.0024 Å

    Correct Answer
    A. 0.024 Å
    Explanation
    The Compton wavelength for an electron is a fundamental constant in quantum mechanics that represents the wavelength associated with the momentum of an electron. It is given by the equation λ = h/mc, where h is Planck's constant, m is the mass of the electron, and c is the speed of light. The correct answer of 0.024 Å indicates that the Compton wavelength for an electron is 0.024 angstroms, which is a very small distance, highlighting the wave-particle duality of electrons.

    Rate this question:

  • 20. 

    Wien's radiation law explains well the blackbody spectrum at

    • Higher temperature

    • All temperatures

    • Higher wavelength

    • Lower wavelength

    Correct Answer
    A. Lower wavelength
    Explanation
    Wien's radiation law states that the wavelength of maximum intensity of radiation emitted by a blackbody is inversely proportional to its temperature. As the temperature increases, the peak of the blackbody spectrum shifts towards shorter wavelengths, meaning lower wavelength. Therefore, the correct answer is lower wavelength.

    Rate this question:

  • 21. 

    The absorptive power of a blackbody is

    • Zero

    • ∞

    • 1

    • 1/2

    Correct Answer
    A. 1
    Explanation
    The absorptive power of a blackbody is 1 because a blackbody is an idealized object that absorbs all incident radiation. It does not reflect or transmit any radiation, hence its absorptive power is maximum, which is 1.

    Rate this question:

  • 22. 

    The energy of photons contained in visible light of wavelength 600 nm is

    • 2 eV

    • 2 keV

    • 2 MeV

    • 0.02 eV

    Correct Answer
    A. 2 eV
    Explanation
    The energy of a photon is given by the equation E = hc/λ, where E is the energy, h is Planck's constant, c is the speed of light, and λ is the wavelength. In this case, the wavelength is given as 600 nm. Plugging in the values, we can calculate the energy of the photon to be approximately 2 eV (electron volts).

    Rate this question:

  • 23. 

    The Compton wavelength for a particle of mass M is given by

    • (h/Mc)²

    • H/(Mc²)

    • H/(Mc)

    • Mc²/h

    Correct Answer
    A. H/(Mc)
    Explanation
    The Compton wavelength is a fundamental concept in quantum mechanics that describes the wavelength associated with a particle of mass M. It is given by the expression h/(Mc), where h is the Planck constant and c is the speed of light. This expression represents the ratio of the Planck constant to the product of the mass and the speed of light. Therefore, the correct answer is h/(Mc).

    Rate this question:

  • 24. 

    What is the speed of a particle whose mass is 3 times its rest mass?

    • 2c/3

    • C/3

    • √2c

    • 2√2c/3

    Correct Answer
    A. 2√2c/3
    Explanation
    The speed of a particle is given by the equation v = √(1 - (m₀/m)²) * c, where v is the speed of the particle, m₀ is the rest mass of the particle, m is the mass of the particle, and c is the speed of light. In this case, the mass of the particle is 3 times its rest mass, so m = 3m₀. Plugging this into the equation, we get v = √(1 - (m₀/(3m₀))²) * c = √(1 - 1/9) * c = √(8/9) * c = √8/√9 * c = 2√2/3 * c. Therefore, the speed of the particle is 2√2c/3.

    Rate this question:

  • 25. 

    The momentum of an electron (rest mass energy = 0.5 MeV) is 1 MeV/c. Its energy in MeV is

    • 1.5

    • 1.12

    • 1.22

    • 2.22

    Correct Answer
    A. 1.12
    Explanation
    The energy of an electron can be calculated using the equation E = mc^2, where E is the energy, m is the rest mass energy, and c is the speed of light. Given that the rest mass energy of the electron is 0.5 MeV and the momentum is 1 MeV/c, we can calculate the energy using the equation E = sqrt((mc^2)^2 + (pc)^2), where p is the momentum. Plugging in the values, we get E = sqrt((0.5 MeV)^2 + (1 MeV/c)^2) = 1.12 MeV. Therefore, the energy of the electron is 1.12 MeV.

    Rate this question:

  • 26. 

    1 milligram of matter after getting converted into energy will yield

    • 9x10¹⁰ Joules

    • 300 Joules

    • 9x10¹³ Joules

    • 900 Joules

    Correct Answer
    A. 9x10¹⁰ Joules
    Explanation
    When matter is converted into energy, the amount of energy produced can be calculated using Einstein's famous equation E=mc², where E represents energy, m represents mass, and c represents the speed of light. In this case, we are given that 1 milligram of matter is being converted into energy. Since the speed of light is a constant, the energy produced will be directly proportional to the mass. Therefore, 1 milligram of matter will yield 9x10¹⁰ Joules of energy.

    Rate this question:

  • 27. 

    A particle (with rest mass m₀) moving at 60% the speed of light has a relativistic mass of

    • 1.67 m₀

    • 1.25 m₀

    • 0.8 m₀

    • 0.6 m₀

    Correct Answer
    A. 1.25 m₀
    Explanation
    When an object moves at a significant fraction of the speed of light, its mass increases due to relativistic effects. This increase in mass is given by the equation m = γm₀, where m₀ is the rest mass, γ is the Lorentz factor, and m is the relativistic mass. The Lorentz factor is calculated as γ = 1/√(1 - (v/c)²), where v is the velocity of the object and c is the speed of light. In this case, the particle is moving at 60% the speed of light, so v/c = 0.6. Plugging this value into the equation, we find γ = 1.25. Therefore, the particle's relativistic mass is 1.25 times its rest mass, which is represented by the answer 1.25 m₀.

    Rate this question:

  • 28. 

    The de Broglie wavelength of an electron accelerated by a potential of 150 V is

    • 0.08 Å

    • 1 Å

    • 12.26 Å

    • 150 Å

    Correct Answer
    A. 1 Å
    Explanation
    The de Broglie wavelength of a particle is given by the equation λ = h / p, where λ is the wavelength, h is the Planck constant, and p is the momentum of the particle. In this case, the electron is accelerated by a potential of 150 V, which means it gains kinetic energy. Using the equation for the kinetic energy of an electron, KE = (1/2)mv^2, where m is the mass of the electron and v is its velocity, we can find the momentum of the electron. Since the electron is accelerated by a potential, we can assume it is initially at rest and only has kinetic energy due to the potential. Thus, the momentum can be calculated as p = √(2mKE). Plugging in the given values and solving for p, we can then use the de Broglie wavelength equation to find the wavelength. The correct answer is 1 Å.

    Rate this question:

  • 29. 

    Knowing Wien's constant = 2.9x10⁻³ mK, an estimate of the surface temperature of a star which gives off light of wavelength 400 nm is

    • 7250 K

    • 8750 K

    • 3550 K

    • 5200 K

    Correct Answer
    A. 7250 K
    Explanation
    Wien's law states that the wavelength of the peak intensity of light emitted by a black body is inversely proportional to its temperature. The formula is given by λmax = b/T, where λmax is the wavelength of peak intensity, b is Wien's constant, and T is the temperature in Kelvin. In this question, we are given the wavelength of light emitted by the star (400 nm) and the value of Wien's constant. By rearranging the formula, we can solve for T, which gives us T = b/λmax. Plugging in the values, we get T = (2.9x10⁻³ mK)/(400 nm) = 7250 K. Therefore, the surface temperature of the star is estimated to be 7250 K.

    Rate this question:

  • 30. 

    According to Rayleigh-Jeans' radiation law, the emissive power of a blackbody over a wavelength range λ to λ+dλ is proportional to λⁿ. Then n is

    • 4

    • 1

    • -2

    • -4

    Correct Answer
    A. -4
    Explanation
    According to Rayleigh-Jeans' radiation law, the emissive power of a blackbody over a wavelength range λ to λ+dλ is proportional to λⁿ. In this case, since the question asks for the value of n, we need to determine the relationship between the emissive power and the wavelength. The Rayleigh-Jeans' radiation law states that as the wavelength increases, the emissive power decreases. This is because the energy of the radiation decreases as the wavelength increases. Therefore, the value of n must be negative. Since the question asks for the value of n that is proportional to λⁿ, the correct answer is -4.

    Rate this question:

  • 31. 

    GaP, a semiconductor with an energy gap of 2.25 eV, is used to make LEDs. The wavelength of emitted light from pure GaP is

    • 705 nm

    • 515 nm

    • 630 nm

    • 555 nm

    Correct Answer
    A. 555 nm
    Explanation
    The wavelength of light emitted from a pure GaP semiconductor with an energy gap of 2.25 eV is 555 nm. This is because the energy gap of a material determines the energy of the photons it can emit, and the energy of a photon is inversely proportional to its wavelength. As GaP has a larger energy gap compared to other options, it emits light with a shorter wavelength, which corresponds to the color green.

    Rate this question:

  • 32. 

    The Compton shift Δλ is half the Compton wavelength if the scattering angle is

    • 45°

    • 90°

    • 60°

    • 180°

    Correct Answer
    A. 60°
    Explanation
    The Compton shift Δλ is half the Compton wavelength if the scattering angle is 60°. This is because the Compton shift is the change in wavelength of a photon after it undergoes Compton scattering, which is the interaction between a photon and a charged particle. The Compton wavelength is a fundamental constant that relates the mass of a particle to its wavelength. When the scattering angle is 60°, the change in wavelength is half of the Compton wavelength, indicating a significant shift in the photon's energy and momentum.

    Rate this question:

  • 33. 

    If the uncertainties in velocities of two particles A and B with mass 1.0 x 10ˉ²⁷ kg and 1.0 x 10ˉ³¹ kg respectively are same, the ratio of uncertainties in the positions of A and B is:

    • 1000:1

    • 10000:1

    • 1:1000

    • 1:10000

    Correct Answer
    A. 1:10000
    Explanation
    The ratio of uncertainties in the positions of particles A and B is 1:10000. This means that the uncertainty in the position of particle A is 10000 times smaller than the uncertainty in the position of particle B. Since the uncertainties in velocities of both particles are the same, the ratio of uncertainties in their positions is solely determined by the ratio of their masses. Particle A has a mass of 1.0 x 10ˉ²⁷ kg, while particle B has a mass of 1.0 x 10ˉ³¹ kg. The larger mass of particle B causes a much smaller uncertainty in its position compared to particle A, resulting in the given ratio.

    Rate this question:

  • 34. 

    A proton accelerated through a potential difference of V has the same de Broglie wavelength as an α-particle subjected to a potential difference of

    • 4V

    • V/4

    • V/8

    • 8V

    Correct Answer
    A. V/8
    Explanation
    The de Broglie wavelength of a particle is inversely proportional to its momentum. Since the proton and α-particle have the same de Broglie wavelength, their momenta must be equal. The momentum of a particle is given by its mass multiplied by its velocity. Since the mass of the α-particle is four times that of the proton, the velocity of the α-particle must be one-fourth that of the proton. The potential difference is directly proportional to the kinetic energy of the particle, which is given by 1/2mv^2. Therefore, if the velocity of the α-particle is one-fourth that of the proton, the potential difference for the α-particle must be one-fourth that of the proton, which is V/4.

    Rate this question:

  • 35. 

    The de Broglie wavelength of a tennis balls of mass 60 g moving with a velocity of 10 m/s is approximately:

    • 10ˉ³¹ m

    • 10ˉ³³ m

    • 10ˉ¹⁸ m

    • 10ˉ²⁵ m

    Correct Answer
    A. 10ˉ³³ m
    Explanation
    The de Broglie wavelength of a tennis ball can be calculated using the equation λ = h / (mv), where λ is the wavelength, h is Planck's constant, m is the mass of the tennis ball, and v is its velocity. Given that the mass of the tennis ball is 60 g (or 0.06 kg) and its velocity is 10 m/s, we can substitute these values into the equation to find the wavelength. Using the given values, we find that the de Broglie wavelength is approximately 10ˉ³³ m.

    Rate this question:

  • 36. 

    The wavelength of emitted radiation at temperture T, for which the emissive power of a blackbody becomes maximum is proportional to

    • T²

    • T⁴

    • T⁻⁴

    • T⁻¹

    Correct Answer
    A. T⁻¹
    Explanation
    The wavelength of emitted radiation at temperature T is inversely proportional to T. This is known as Wien's displacement law, which states that as the temperature of a blackbody increases, the peak wavelength of its emitted radiation decreases. This relationship is described by the equation λmax = b/T, where λmax is the peak wavelength, T is the temperature, and b is a constant. Therefore, the correct answer is T⁻¹.

    Rate this question:

  • 37. 

    Compton scattering is performed on blocks of carbon and silver. If I and I' are the intensities of the unmodified (λ) and Compton-shifted (λ') lines in the scattered X-rays, then

    • I > I' for both carbon and silver

    • I = I' for both carbon and silver

    • I > I' for carbon, I < I' for silver

    • I < I' for carbon, I > I' for silver

    Correct Answer
    A. I < I' for carbon, I > I' for silver
    Explanation
    Compton scattering refers to the phenomenon where X-ray photons are scattered by electrons, resulting in a shift in the wavelength of the scattered photons. In this scenario, the question is asking about the intensities of the unmodified and Compton-shifted lines in the scattered X-rays for carbon and silver.

    The correct answer states that I < I' for carbon, I > I' for silver. This means that the intensity of the unmodified line (λ) is less than the intensity of the Compton-shifted line (λ') for carbon, while the intensity of the unmodified line is greater than the intensity of the Compton-shifted line for silver. This suggests that the scattering of X-rays by electrons in carbon leads to a greater shift in wavelength compared to silver.

    Rate this question:

  • 38. 

    Uncertainty in position of a particle of 25 g in space is 10ˉ ⁵ m. Hence, uncertainty in velocity (m sˉ¹) is:

    • 2.1x10ˉ²⁸

    • 2.1x10ˉ³⁴

    • 0.5x10ˉ³⁴

    • 5.0x10ˉ²⁴

    Correct Answer
    A. 2.1x10ˉ²⁸
    Explanation
    The uncertainty principle states that there is a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position and momentum, can be known simultaneously. The uncertainty in position and momentum is related by the equation Δx * Δp ≥ h/4π, where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is Planck's constant. In this case, the uncertainty in position is given as 10ˉ⁵ m. Since the mass of the particle is given as 25 g, we can calculate the uncertainty in momentum using the equation Δp = m * Δv, where Δv is the uncertainty in velocity. Plugging in the values, we get Δp = 0.025 kg * Δv. Solving for Δv, we find Δv = 10ˉ⁵ m / 0.025 kg = 4 x 10ˉ⁶ m/s. Therefore, the uncertainty in velocity is 4 x 10ˉ⁶ m/s, which is equivalent to 4 x 10ˉ²⁸ m/s in scientific notation.

    Rate this question:

  • 39. 

    The uncertainties in the velocities of two particles A and B are 0.05 and 0.02 m sˉ¹ respectively. The mass of B is five times to that of mass A. What is the ratio of uncertainties?

    • 2

    • 0.25

    • 4

    • 1

    Correct Answer
    A. 2
    Explanation
    The ratio of uncertainties is 2. This can be determined by dividing the uncertainty in velocity of particle B (0.02 m/s) by the uncertainty in velocity of particle A (0.05 m/s). Since the mass of B is five times that of A, the uncertainty ratio is equal to the mass ratio, which is 5. Therefore, the ratio of uncertainties is 5/2, which simplifies to 2.

    Rate this question:

  • 40. 

    If the measured momentum of an electron is 3.20 x10ˉ²⁷ kg-m/s with an uncertainty of 1.6 x10ˉ²⁹ kg-m/s, what is the minimum uncertainty in the determination of its position?

    • 1.3 nanometer

    • 1.3 micrometer

    • 3.3 nanometer

    • 3.3 micrometer

    Correct Answer
    A. 3.3 micrometer
    Explanation
    The minimum uncertainty in the determination of the electron's position can be found using the Heisenberg uncertainty principle. According to the principle, the product of the uncertainties in position and momentum must be greater than or equal to Planck's constant divided by 4π. In this case, the uncertainty in momentum is given as 1.6 x 10ˉ²⁹ kg-m/s. By rearranging the equation, we can solve for the uncertainty in position. Plugging in the given values, we find that the minimum uncertainty in the determination of the electron's position is 3.3 micrometers.

    Rate this question:

  • 41. 

    The de Broglie wavelengths of electron waves in two orbits is 3:5. The ratio of kinetic energy of electrons will be: 

    • 5:3

    • 3:5

    • 25:9

    • 9:25

    Correct Answer
    A. 25:9
    Explanation
    The de Broglie wavelength is inversely proportional to the momentum of the electron. Since the de Broglie wavelengths of the electron waves in two orbits are in the ratio of 3:5, the momentum of the electrons in the two orbits will be in the inverse ratio of 3:5. Since kinetic energy is directly proportional to the square of the momentum, the ratio of kinetic energies will be the square of the inverse ratio of momentum, which is (5/3)^2 = 25:9.

    Rate this question:

Quiz Review Timeline (Updated): Mar 21, 2023 +

Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.

  • Current Version
  • Mar 21, 2023
    Quiz Edited by
    ProProfs Editorial Team
  • Mar 22, 2015
    Quiz Created by
    Saptarshi Ghosh
Back to Top Back to top
Advertisement
×

Wait!
Here's an interesting quiz for you.

We have other quizzes matching your interest.