An image formed when the light rays pass through the image location,...
If the magnification is a negative value, the image is
If the absolute value of the magnification is equal to one, then the...
A spherical mirror on which reflection takes place on the outer...
If the image distance is positive, the image formed is a
A spherical mirror on which reflection takes place on the inner...
If the image distance is negative, the image formed is a
Light travels fastest
An image formed when the light rays do not actually pass through the...
If the magnification is a positive value, the image is
If the absolute value of the magnification is smaller than one, then...
Lenses that are thinner at the center than the edges are called
Lenses that are thickest at the center called
The principle on which lenses work is
A object is 12 cm in front of a concave mirror, and the image is 3.0...
If the absolute value of the magnification is larger than one, then...
Plane mirrors produce images which
A concave mirror with a radius of 20 cm creates a real image 30 cm...
Two diverging lenses are similar except that lens B is rated at 20...
Light arriving at a concave mirror on a path parallel to the axis is...
A beam of light, traveling in air, strikes a plate of transparent...
A spherical concave mirror has a radius of curvature of 20 cm. How far...
An object is situated between a concave mirror's surface and its...
An object is 10.4 cm tall, and 4.8 cm in front of a diverging lens....
A object is placed between a convex lens and its focal point. The...
The principle on which mirrors work is
Lucite has an index of refraction of 1.50. What is its critical angle...
A single convex spherical mirror produces an image which is
A ray of light, which is traveling in air, is incident on a glass...
The principle on which fiber optics is based is
An object is located 2.6 m in front of a plane mirror. The image...
A substance has an index of refraction of 1.46. Light is passing...
An object is 5.7 cm from a concave mirror. The image is 4.7 cm tall,...
How far from a lens of focal length 50 mm must the object be placed if...
An object is placed 40 cm in front of a 20 cm focal length converging...
An object is 47.5 cm tall. The image is 38.6 cm tall, and 14.8 cm from...
A biconvex lens is formed by using a piece of plastic (n = 1.70). The...
If the radius of curvature of the concave mirror is r, the focal...
The angle of incidence
An optic fiber is made of clear plastic with index of refraction of...
Light enters a substance from air at 30.0° to the normal. It...
A concave spherical mirror has a focal length of 20 cm. An object is...
Is it possible to see a virtual image?
A light ray, traveling parallel to a concave mirror's axis,...
An image is 4.0 cm behind a concave mirror with focal length 5.0 cm....
When an object is 40 m in front of a converging lens the inverted...
A 1.4 cm tall object is 4.0 cm from a concave mirror. If the image is...
If a material has an index of refraction of 1.50, what is the speed of...
A convex lens has a focal length f. An object is placed between...
Lenses that are thicker at the center
What is the critical angle for light traveling from crown glass (n =...
If you stand in front of a convex mirror, at the same distance from it...
An object is 12 cm in front of a converging lens with focal length 4...
The critical angle for a beam of light passing from water into air is...
If you stand in front of a concave mirror, exactly at its focal point,
Light enters a substance from air at an angle of 32.0°, and...
Light passes from air to water. The incoming ray is at an angle of...
An oil layer that is 5.0 cm thick is spread smoothly and evenly over...
An object is 6.0 cm tall, and is in front of a diverging lens. The...
An object is placed at a concave mirror's center of curvature. The...
A convex lens has focal length f. An object is placed at 2f on the...
Sometimes when you look into a curved mirror you see a magnified image...
An object is placed at a distance of 30 cm from a thin convex lens....
A person's face is 30 cm in front of a concave shaving mirror. If...
A convex lens has focal length f. An object is located at infinity....
A light ray, traveling obliquely to a concave mirror's surface,...
A diver is 1.2 m beneath the surface of a still pond of water. At what...
A double convex lens made of glass (n = 1.50) has a radius of 40 cm on...
Light traveling at an angle into a denser medium is refracted
The image of the rare stamp you see through a magnifying glass is
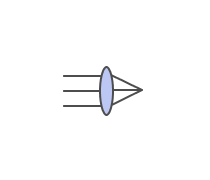
A light ray, traveling parallel to the axis of a convex thin lens,...
If you stand in front of a convex mirror, at the same distance from it...
A 14-mm tall object is 4.0 mm from a converging lens. If the image is...
Light enters air from water. The angle of refraction will be
A convex lens has a focal length f. An object is placed at f on the...
An object is placed at 30 cm in front of a diverging lens with a focal...
Reflection, refraction, and the formation of images by mirrors and...
An object is placed 15 cm from a concave mirror of focal length 20 cm....
For all transparent material substances, the index of refraction
The index of refraction of diamond is 2.42. This means that a given...
When a person stands 40 cm in front of a cosmetic mirror (concave...
How far are you from your image when you stand 0.75 m in front of a...
An optical fiber is 1.0 meter long and has a diameter of 20 μm. Its...
When an object is placed 60 cm from a converging lens, it forms a real...
A plano-convex lens is to have a focal length of 40 cm. It is made of...
A light ray in air is incident on an air to glass interface at an...
A plane mirror forms an image that is
The critical angle for a substance is measured at 53.7°. Light...
Concave spherical mirrors produce images which
An object is 15.2 mm from a converging lens. The image is 4.0 mm tall,...
Convex spherical mirrors produce images which
An object is placed at 30 cm in front of a diverging lens with a focal...
A double convex (convex-convex) thin lens has radii of curvature 46...
An object is 14 cm in front of a convex mirror. The image is 5.8 cm...
Light arriving at a concave mirror on a path through the focal point...
An image is 4.0 mm in front of a converging lens with focal length 5.0...
A laser beam strikes a plane's reflecting surface with an angle of...
An index of refraction less than one for a medium would imply
The images formed by concave lenses
A beam of light traveling in air is incident on a slab of transparent...
A concave spherical mirror has a focal length of 20 cm. An object is...
An object is positioned between a concave mirror's center of...
How far from a 50-mm focal length lens, such as is used in many 35-mm...
A convex spherical mirror has a focal length of -20 cm. An object is...
An object is 8.90 cm tall. The image is 7.80 cm tall, and 14.8 cm from...
A negative magnification for a mirror means
The angle of incidence
An object is placed 15 cm from a concave mirror of focal length 20 cm....
Two very thin lenses, each with focal length 20 cm, are placed in...
A light ray, traveling obliquely to a concave mirror's axis,...
A convex lens has a focal length f. An object is placed between f and...
An object is placed at a distance of 40 cm from a thin lens. If a...
Light arriving at a concave mirror on a path through the center of...
An object is 4.1 cm tall, and 10.3 cm from a converging lens. The...
A light ray, traveling parallel to the axis of a thin concave lens,...
How fast do you approach your image when you approach a vertical plane...
Two thin double-convex (convex-convex) lenses are placed in contact....
An object is 10 cm in front of a concave mirror with focal length 3...
A single concave spherical mirror produces an image which is
A convex spherical mirror has a focal length of -20 cm. An object is...
A lamp is placed 1 m from a screen. Between the lamp and the screen is...
An object is 15 mm in front of a converging lens, and the image is 4.0...
A diverging lens (f = -4.0 cm) is positioned 2.0 cm to the left of a...
Two thin lenses, of focal lengths f1 and f2 placed in contact with...