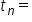Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
What is the common difference for the sequence above?.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
Using the sequence above, determine the value of 'd'.
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
Above is an Arithmetic Series - a sequence of numbers added together....
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
What is the common difference for the sequence above?.
For the above sequence, what is the value of term number 36?
For the above sequence, what is the value of term number 25?
For the above sequence, what is the value of term number 25?
For the above sequence, what is the value of term number 35?
For the above sequence, what is the value of term number 36?
For the above sequence, what is the value of term number 33?
For the above sequence, what is the value of term number 20?
For the above sequence, what is the value of term number 36?
For the above sequence, what is the value of term number 36?
For the above sequence, what is the value of term number 36?
For the above sequence, what is the value of term number 36?
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
Above is an Arithmetic Series - a sequence of numbers added together....
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :
For the sequence above, the rule for the arithmetic sequence is :