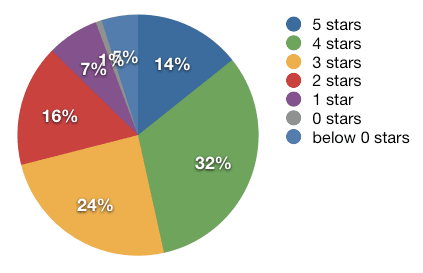Review For The Algebra 2 [ac] Semester 2 Final Exam Part 1: Chapters 10-11
-
The distance between the points (2,1) and (6,4) is:
I'll be quizzing and giving y'all some formulas through chapters 10-11 (focusing on conic sections and probability).
![Review For The Algebra 2 [ac] Semester 2 Final Exam Part 1: Chapters 10-11 - Quiz Review For The Algebra 2 [ac] Semester 2 Final Exam Part 1: Chapters 10-11 - Quiz](https://media.proprofs.com/images/QM/user_images/1826446/New%20Project%20(22)(178).webp)
Quiz Preview
- 2.
Write the equation of the circle with center (3, 7) and containing the point (11, 13).
Explanation
1. Use the distance formula to find the radius of the circle.
2. Substitute the values into the equation of a circle:
The equation of a circle with center (h, k) and radius r is (x-h)^2 + (y-k)^2 = r^2
As r=10, x=3, and y=7, your formula will be [hopefully posted in the answer box, and] (x-3)^2+(y-7)^2=100.Rate this question:
- 3.
1.A/n _______ is the set of points in a plane such that the sum of the distances from any point on the _____ to two fixd points (the foci) is the constant sum. 2.A/n _______ is the set of points in a plane such that the difference of the distances from P to fixed points F1 and F2, the foci, is constant. 3.A/n _______ is the set of all points in a plane that are an equal distance from both a fixed point, the focus, and a fixed line, the directrix.
Explanation
So the formulas for these superbly amazing conic sections are (besides the circle; we've already done that one):
Horizontal Axis Vertical Axis
Ellipse: ((x-h)^2)/a^2 + ((y-k)^2)/b^2=1 ((x-h)^2)/b^2 + ((y-k)^2)/a^2=1
Hyperbola: ((x-h)^2)/a^2 - ((y-k)^2)/b^2=1 ((y-k)^2)/a^2 - ((x-h)^2)/b^2=1
Parabola: x-h = (1/(4p))(y-k)^2 y-k = (1/(4p))(x-h)^2
In all of those formulas, co-vertices are represented by b, vertices by a, and foci by c.Rate this question:
- 4.
Classifying Conic Sections: B2-4AC < 0 and either B=0, and A=C (in the form of Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0) is a circle.
-
True
-
Maybe.
Correct Answer
A. TrueExplanation
If B2-4AC < 0 and either B=0 and A=C, then the equation is in the form of a circle. This is because the condition B2-4AC < 0 ensures that the equation represents a non-degenerate conic section (not a line or a point), and when B=0 and A=C, the equation simplifies to the standard form of a circle. Therefore, the statement is true.Rate this question:
-
- 5.
Find the probability that the red cube shows a 5 and that the sum of the red cube and the orange cube is less than or equal to 8.
-
1/6
-
1/12
-
1/3
-
3/24
-
3/12
Correct Answer
A. 1/12Explanation
Dependent events: P(A and B) = P(A) x P(B given A)
1/6 that red cube shows a 5
6, 7, 8,Rate this question:
-
- 6.
Find the probability with a general dice of rolling at least one 4 when rolling 2 dice:
-
1/36
-
1/6
-
11/36
-
1/9
Correct Answer
A. 11/36Explanation
P(4 or 4) = P(4) + P(4) - P(4 and 4), given the formula P (A or B) = P (A) + P (B) - P(A and B).Rate this question:
-
- 7.
MATCHING: So, we've already got the equations of all the basic conics. Now for the location of the vertices, foci, and co-vertices. Y'all will now match: For a horizontal A, vertices are (h+a, k) and (h-a, k); foci are (h+c, k) and (h-c, k); co-vertices are (h, k+b) and (h, k-b); asymptotes are y-k= (+/-)b/a(x-h) For a horizontal B, the focus is (h+p, k), and the directrix is x=h-p For a horizontal C, the vertices are (h+a, k) and (h-a, k); foci are (h+c, k) and (h-c, k); co-vertices are (h, k+b) and (h, k-b). The below answers are listed as the projected guesses for A, B, and C in that order.
-
Ellipse, Parabola, Hyperbola
-
Hyperbola, Ellipse, Parabola
-
Parabola, Hyperbola, Ellipse
-
Parabola, Ellipse, Hyperbola
Correct Answer
A. Parabola, Hyperbola, EllipseExplanation
The given answer is Parabola, Hyperbola, Ellipse. This is because the first set of information describes a parabola, with the focus and directrix given. The second set of information describes a hyperbola, with the vertices, foci, and co-vertices given. The third set of information describes an ellipse, with the vertices, foci, and co-vertices given. Therefore, the correct order is Parabola, Hyperbola, Ellipse.Rate this question:
-
- 8.
The midpoint of the segment with endpoints (4, 8) and (-11, -2) is ______.
Correct Answer
(-3.5, 3)
(-7/2, 3)Explanation
The midpoint of a segment is found by taking the average of the x-coordinates and the average of the y-coordinates of the endpoints. For the given endpoints (4, 8) and (-11, -2), the average of the x-coordinates is (4 + (-11))/2 = -7/2 and the average of the y-coordinates is (8 + (-2))/2 = 3. Therefore, the midpoint is (-7/2, 3). Additionally, this can also be written as (-3.5, 3) since -7/2 is equal to -3.5.Rate this question:
- 9.
Classifying Conic Sections: B2-4AC=0 in the form of Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 is a parabola.
-
True
-
False
Correct Answer
A. TrueExplanation
The equation B^2 - 4AC = 0 is the discriminant of a quadratic equation, and when it is in the form of Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, it represents a conic section. When the discriminant is zero, it indicates that the conic section is a parabola. Therefore, the given statement "B2-4AC=0 in the form of Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 is a parabola" is true.Rate this question:
-
- 10.
Classifying Conic Sections: B2-4AC=0 in the form of Ax^2 + Bxy + Cy^2 + Dx + Ey + F > 0 is a hyperbola.
-
Yes
-
No
Correct Answer
A. YesExplanation
The equation B2-4AC=0 in the given form represents a conic section. A hyperbola is a type of conic section, so if the equation satisfies this condition, it can be classified as a hyperbola. Therefore, the correct answer is Yes.Rate this question:
-
- 11.
Classifying Conic Sections: B2-4AC < 0 and either B is not equal to 0 or A is not equal to C (in the form of Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0) is a circle.
-
True
-
False--- no way man, that's an ellipse!
Correct Answer
A. False--- no way man, that's an ellipse!Explanation
You bet it is an ellipse!Rate this question:
-
- 12.
Combination: order does not matter. Permutation: order does indeed matter. nCr = n! / r!(n-r)! <-- that is indeed a combination formula. Permutation's easier, do you know that one? What is the probability of an event happening? Answer only the second question please.
-
Yes
-
Number of favorable outcomes / number of outcomes in the sample space
-
Number of possible ways to have something happen / number of ways scientists have thought smart thinkers to the moon to contemplate.
Correct Answer
A. Number of favorable outcomes / number of outcomes in the sample spaceExplanation
The correct answer is "number of favorable outcomes / number of outcomes in the sample space". This is the formula for calculating the probability of an event happening. It represents the ratio of the number of favorable outcomes (outcomes that satisfy the event) to the total number of outcomes in the sample space (all possible outcomes).Rate this question:
-
- 13.
Inclusive events are events that have one or more outcome in common. A simple event is an event that describes a single outcome. A compound event is an event made up of one or more simple events. Mutually exclusive events are events that cannot both occur in the same trial of an experiment (like rolling a 1 and a 2 on the same roll).
-
True
-
False
Correct Answer
A. FalseExplanation
Just kidding, guys. Everything's true except that the third line, where it should be, "A compound event is an event made up of TWO or more simple events."Rate this question:
-
- 14.
Write an equation in standard form for the below ellipse with center (0,0): an ellipse with vertex (0,8) and co-vertex (3,0). No spaces, and recognize all 'squared' symbols as I have been, for instances x2 is equal to x^2.
Correct Answer
y^2/64+x^2/9=1Explanation
Step 1. The vertex is on the y-axis.
Step 2. Identify the values of a and b ; a=8, b=3.
Step 3. Write the equation.Rate this question:
- 15.
Let's talk about nonlinear system of equations; rhar is a system in which at least one of the equations is not linear; a class of which is the conic sectiosn. You can solve these bad boys by graphing, substitution, and elimination, and the points you'll finally settle down with are the intersection points between the equations in your system. It appears that most of them are conic section and some other sort of linear or nonlinear equation.
-
Sounds legit.
-
Okay, cool. Next?
-
Oh, dear. Next is probability.
Correct Answer
A. Oh, dear. Next is probability. -
- 16.
Each student received a 4-digit code to use the library computers, with no digit repeated. Manu received the code 7654. What was the probability that he would receive a code of consecutive numbers?
Correct Answer
1/360
14/540Explanation
1. Order is important, so this is a permutation.
2. Find the number of outcomes in the sample space. The sample space is the number of permutations of 4 of 10 digits; 10P4.
3. Then you just count out the seven numbers that are consecutive and the reverse of these to get 14/10P4, or `14/540, or 1/360.Rate this question:
- 17.
You roll a dice (basic; numbered 1-6) twice. What is the probability that you will roll one number which is a prime number (not 1), and then roll a number greater than four but less than seven?
Correct Answer
1/6Explanation
If A and B are independent events, then P(A and B) = P(A) x P(B).
2, 3, 5, are prime numbers (1/2)
5, 6 form a 2 in 6 chance (1/3)
1/3 x 1/2 is 1/6.Rate this question:
- 18.
Round to the second decimal place: There are 4 students in a music-listening-to club. Each student randomly chooses an album from a list of 8 titles. What is the probability that at least 2 of the students in the group choose the same book?
Correct Answer
0.59
59%Explanation
Use the complement!
P(all choose different) = number of ways 4 students can choose different albums / total number of ways 4 students can choose albums
=8P4/8^4
=0.41015625
1 - 0.41015625 = about 0.59Rate this question:
- 19.
Find the mode and median in your lovely and very intelligent head. Then, find the weighted average of stars for a movie. But, ignore the category saying below 0 stars; this will involve taking 0.07 out. Keep it in mind, kay? Round to two decimal places.
Correct Answer
3.32Explanation
0.14(5)+0.32(4)+0.24(3)+0.16(2)+0.07(1)+0.01(0)=3.09
3.09 divided by 0.93 is then equal to 3.32258065Rate this question:
- 20.
Final question! *There are no binomial distributions on our final, she said so herself. Take the data values 1, 1, 6, 4, 8, 3, 6, and 3. Then find the standard deviation of the data. Round to four decimal places.
Correct Answer
2.3452Explanation
1, 1, 6, 4, 8, 3, 6, and 3.
Mean: 4
Find the difference between the mean and each value:
3, 3, 2, 0, 4, 1, 2, and 1.
Square each of these values and then add them together:
9+9+4+0+16+1+4+1=44
Then divide that number by the number of data values:
44/8=5.5
That's the variance. For the standard deviation, take the square root of the variance;
2.34520788
Rounded:
2.3452Rate this question:
Quiz Review Timeline (Updated): May 13, 2024 +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
May 13, 2024Quiz Edited by
ProProfs Editorial Team -
Jun 13, 2011Quiz Created by
Alg2victims4lyf
A Mathematical Exam About Ellipse & Hyperbola. Be A Mathematician
A hyperbola is an open curve with two branches, the intersection of a plane with both halves of a double cone. The plane does not have to be parallel to the axis of the...
Questions:
8 |
Attempts:
311 |
Last updated:
Dec 17, 2024
|
Conic Sections And Circles
Explore the fundamentals of geometry with our 'Conic Sections and Circles' quiz. Test your knowledge on circle equations, centers, radii, and the properties of conics. Ideal for...
Questions:
10 |
Attempts:
81 |
Last updated:
Dec 27, 2024
|
Conic Sections And Introduction To Circles
Explore the fundamentals of geometry with our 'Conic Sections and Introduction to Circles' quiz. This quiz assesses your understanding of circle equations, centers, radii, and the...
Questions:
10 |
Attempts:
75 |
Last updated:
Mar 03, 2023
|
Conic Sections And Circle
This is an assessment if you really understood the lesson about Conic sections and Circles
Questions:
11 |
Attempts:
2071 |
Last updated:
Dec 27, 2024
|
What Do You Know About Conic Sections?
In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. Take the quiz to...
Questions:
10 |
Attempts:
190 |
Last updated:
Mar 20, 2023
|
Polynomial Long Division Quiz
How strong is your math? Can you score high on this polynomial long division quiz? In algebra, the long polynomial division is meant by an algorithm that is used for dividing a...
Questions:
10 |
Attempts:
606 |
Last updated:
Feb 12, 2024
|
 Back to top
Back to top