What Is Division Key Concepts, Strategies, and Solved Problems? Definition, Examples & Key Concepts
Lesson Overview
Division is one of the four fundamental operations in mathematics, used to split quantities into equal parts or determine how many times one number fits into another. In this lesson, you will explore the core concepts of division, including terms like dividend, divisor, quotient, and remainder. You'll learn a variety of strategies such as repeated subtraction, equal grouping, long division, and the relationship between multiplication and division.
What Is Division?
Division is a mathematical operation used to split a number into equal parts or to determine how many times one number is contained within another. It is the inverse of multiplication.
Key Terms:
| Term | Definition |
|---|---|
| Dividend | The number being divided |
| Divisor | The number that divides the dividend |
| Quotient | The result of the division |
| Remainder | The leftover part if the division is not exact (optional) |
Symbolic Representation:
- a ÷ b = c
→ a is the dividend, b is the divisor, c is the quotient. - Alternatively:
a⁄b = c
→ read as "a divided by b."
Examples:
- 12 ÷ 3 = 4 → 12 is divided into 3 equal parts of 4.
- 15 ÷ 4 = 3 R3 → 4 fits into 15 three times with a remainder of 3.
Types of Division:
- Exact Division: No remainder (e.g., 20 ÷ 5 = 4)
- Inexact Division: Includes a remainder (e.g., 22 ÷ 7 = 3 R1)
Division is essential in everyday problem-solving, such as sharing items equally, measuring quantities, or distributing resources.
What Are the Various Types of Division?
Division can be classified into different types based on how it is performed, the numbers involved, and the result expected. Understanding these types helps learners approach problems with the correct method and interpretation.
1. Based on Result: Exact vs. Inexact Division
| Type | Description | Example |
|---|---|---|
| Exact Division | The dividend is completely divisible by the divisor, leaving no remainder. | 20 ÷ 5 = 4 |
| Inexact Division | The dividend is not completely divisible; a remainder is left. | 22 ÷ 7 = 3 R1 |
2. Based on Method:
| Type | Description | Example |
|---|---|---|
| Short Division | Quick, mental division for small numbers. | 48 ÷ 4 = 12 |
| Long Division | Step-by-step written method used for large numbers. | 987 ÷ 3 = 329 |
| Repeated Subtraction | Subtract the divisor repeatedly from the dividend until zero or a remainder remains. | 12 ÷ 3 → 12 − 3 − 3 − 3 − 3 = 0 (4 subtractions) |
| Division Using Number Line | Visual method for beginners-jump by divisor on a number line. | 15 ÷ 3 = 5 jumps of 3 |
| Division by Grouping | Objects are grouped to determine how many times the divisor fits in. | 18 divided into groups of 6 = 3 groups |
3. Based on Number Type:
| Type | Description | Example |
|---|---|---|
| Whole Number Division | Division of whole numbers. | 36 ÷ 6 = 6 |
| Decimal Division | Division involving decimals; often requires aligning decimal points. | 4.8 ÷ 1.2 = 4 |
| Fraction Division | Divide by multiplying with the reciprocal of the divisor. | (2⁄3) ÷ (1⁄4) = 2⁄3 × 4⁄1 = 8⁄3 |
| Integer Division | Division involving negative numbers or zero. | –12 ÷ 3 = –4 |
| Algebraic Division | Division involving variables or expressions. | (6x² ÷ 3x = 2x) |
4. Based on Application:
| Type | Use Case |
|---|---|
| Equal Sharing | Used when a quantity is split evenly among groups. |
| Measurement Division | Used to determine how many units of a specific size fit into a total amount. |
What Are the Rules of Division?
Division follows a specific set of rules that ensure accuracy and consistency across mathematical operations. These rules apply to numbers, signs, and special cases involving zero or decimals. Mastering these rules helps in solving division problems correctly across all levels of math.
1. Division by 1 Rule
- Any number divided by 1 is the number itself.
a ÷ 1 = a
Example:
25 ÷ 1 = 25
2. Division of a Number by Itself
- Any number (except 0) divided by itself equals 1.
a ÷ a = 1, where a ≠ 0
Example:
9 ÷ 9 = 1
3. Division of Zero by a Number
- Zero divided by any non-zero number is 0.
0 ÷ a = 0, where a ≠ 0
Example:
0 ÷ 7 = 0
4. Division by Zero (Undefined)
- Dividing any number by 0 is undefined and not allowed in mathematics.
a ÷ 0 = undefined
Example:
6 ÷ 0 → undefined
5. Sign Rule in Division
| Operands | Result Sign |
|---|---|
| Positive ÷ Positive | Positive |
| Negative ÷ Negative | Positive |
| Positive ÷ Negative | Negative |
| Negative ÷ Positive | Negative |
Example:
–12 ÷ 4 = –3
–12 ÷ –4 = 3
6. Division of Decimals
- Align decimals properly or multiply both numbers by 10ⁿ to make the divisor a whole number, then divide.
Example:
4.2 ÷ 0.7 = (42 ÷ 7) = 6
7. Fraction Division Rule
- To divide by a fraction, multiply by its reciprocal.
(a⁄b) ÷ (c⁄d) = (a⁄b) × (d⁄c)
Example:
(2⁄3) ÷ (4⁄5) = (2⁄3) × (5⁄4) = 10⁄12 = 5⁄6
8. Long Division Carry Rule
- If the current digit of the dividend is smaller than the divisor, bring down the next digit to continue.
9. Distributive Property (Reverse Check)
- You can check division with multiplication.
If a ÷ b = c, then c × b = a
Example:
16 ÷ 4 = 4 → 4 × 4 = 16
Take This Quiz
How Do You Divide Fractions?
Rule:
To divide two fractions, multiply the first fraction by the reciprocal of the second.
Formula:
(a⁄b) ÷ (c⁄d) = (a⁄b) × (d⁄c)
Example:
(2⁄3) ÷ (4⁄5) = (2⁄3) × (5⁄4) = 10⁄12 = 5⁄6
Steps:
- Keep the first fraction.
- Flip (take the reciprocal of) the second fraction.
- Multiply the numerators and denominators.
- Simplify the result if possible.
How Do You Divide Decimals?
Rule:
Make the divisor a whole number by multiplying both the dividend and divisor by 10ⁿ (move the decimal point to the right), then divide as with whole numbers.
Formula:
a.b ÷ c.d → (a.b × 10ⁿ) ÷ (c.d × 10ⁿ)
Example:
4.5 ÷ 1.5 = (45 ÷ 15) = 3
Steps:
- Shift the decimal in the divisor to the right until it becomes a whole number.
- Shift the decimal in the dividend the same number of places.
- Perform regular division.
- Place the decimal point correctly in the result.
How Do You Divide Powers?
Rule (Same Base):
When dividing powers with the same base, subtract the exponents.
Formula:
aⁿ ÷ aᵐ = aⁿ⁻ᵐ
Example:
x⁵ ÷ x² = x³
10⁶ ÷ 10³ = 10³
Rule (Different Base or Exponent):
If the bases or exponents are different, evaluate each power first, then divide.
Example:
2³ ÷ 5² = 8 ÷ 25
Take This Quiz
Conclusion
Excellent work on completing this division lesson! You have developed a thorough understanding of division, a critical mathematical operation that underpins much of arithmetic and problem-solving. This lesson on division has guided you through the essential concepts of division, from basic division with whole numbers to more advanced topics such as dividing fractions, decimals, and powers.
Rate this lesson:
 Back to top
Back to top
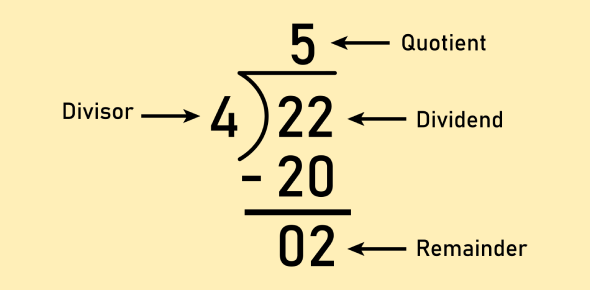
(358).webp)