Addition and Subtraction of Fractions and Decimals

Created by Editorial Team

The ProProfs editorial team is comprised of experienced subject matter experts. They've collectively created over 10,000 quizzes and lessons, serving over 100 million users. Our team includes in-house content moderators and subject matter experts, as well as a global network of rigorously trained contributors. All adhere to our comprehensive editorial guidelines, ensuring the delivery of high-quality content.

Learn about Our Editorial Process

Updated: Apr 17, 2025

Lesson

Lesson Overview

Why Is Understanding Fractions and Decimals Essential?
How Do You Convert Between Fractions and Decimals?
What Are the Methods for Adding Fractions?
How Can You Subtract Fractions?
How Do You Precisely Add Decimals?
How Is Decimal Subtraction Performed Accurately?
What Strategies Help Combine Fractions and Decimals?
What Common Errors Should Be Avoided?
How Do These Concepts Apply to Real-Life Situations?
How Can You Strengthen Critical Thinking with Fraction and Decimal Problems?
Extensive Practice Problems

Imagine you are planning a science experiment requiring precise measurements of chemicals. The slightest miscalculation with fractions and decimals can drastically change your outcomes. This lesson on the Addition and Subtraction of Fractions and Decimals empowers you to handle such critical calculations confidently.

Why Is Understanding Fractions and Decimals Essential?

Fractions and decimals represent partial quantities and are fundamental to precise measurement, data analysis, financial calculations, and various scientific fields. Proficiency in these areas ensures accurate handling of complex quantitative problems encountered academically and practically.

How Do You Convert Between Fractions and Decimals?

Converting fractions and decimals interchangeably helps standardize values, simplify computations, and clearly compare different forms of numerical data.

Converting Fractions to Decimals

To convert a fraction into a decimal, divide the numerator by the denominator:

Example: 3/4 → 3 ÷ 4 = 0.75.

Converting Decimals to Fractions

Decimals can be converted back into fractions by identifying their place value:

Example: 0.25 → 25/100 → 1/4.

Simplifying Fractions

Always simplify fractions to their lowest terms for accurate and clear communication of values.

Example: 4/8 → 1/2.

What Are the Methods for Adding Fractions?

Accurate addition of fractions requires careful attention to denominators and systematic calculation to ensure precision.

Adding Fractions with Common Denominators

Directly add numerators:

Example: 1/5 + 3/5 = 4/5.

Adding Fractions with Different Denominators

Find the least common denominator (LCD), convert fractions accordingly, then add:

Example: 2/3 + 1/4; LCD is 12:
Convert and add: 8/12 + 3/12 = 11/12.

Adding Mixed Numbers

Combine whole numbers separately, then fractions:

Example: 2 1/2 + 3 1/3 → (2 + 3) + (3/6 + 2/6) → 5 5/6.

How Can You Subtract Fractions?

Fraction subtraction relies on finding a common denominator and accurately performing arithmetic operations.

Subtracting Fractions with Common Denominators

Subtract numerators directly:

Example: 7/8 - 3/8 = 4/8 → 1/2.

Subtracting Fractions with Different Denominators

Find LCD, convert, then subtract:

Example: 3/4 - 1/6; LCD is 12:
Convert and subtract: 9/12 - 2/12 = 7/12.

Subtracting Mixed Numbers

Separate whole numbers and fractions for clarity:

Example: 5 2/3 - 2 1/4 → (5 - 2) + (8/12 - 3/12) → 3 5/12.

Take This Quiz!

$Problems with fractions (addition and subtraction)$

Problems with fractions (addition and subtraction)

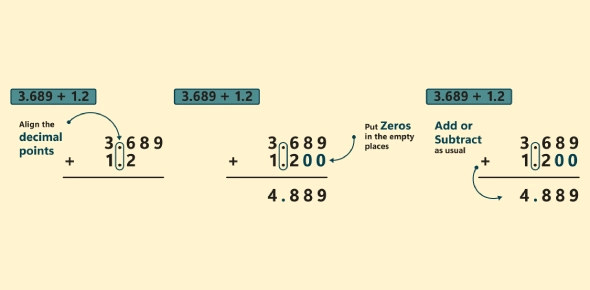
How Do You Precisely Add Decimals?

Precision in decimal addition involves the careful alignment of decimal points and systematic calculation.

Step-by-Step Decimal Addition

Align decimal points.
Add zeros for equal decimal places.
Add vertically.

Example: 5.375 + 1.05: 5.375 +1.050

6.425

How Is Decimal Subtraction Performed Accurately?

As such, decimal subtraction requires precision in alignment and calculation to avoid errors.

Step-by-Step Decimal Subtraction

Align decimal points vertically.
Add zeros as placeholders.
Subtract vertically.

Example: 13.009 - 0.7: 13.009
0.700

12.309

What Strategies Help Combine Fractions and Decimals?

To effectively combine fractions and decimals, convert all numbers into one form, either fractions or decimals, for simplicity and precision.

Converting Fractions to Decimals (Recommended)

Example: 1/4 + 0.25 → 0.25 + 0.25 = 0.50.

Converting Decimals to Fractions

Example: 0.75 + 1/8 → 3/4 + 1/8 → 7/8.

What Common Errors Should Be Avoided?

Common mistakes when working with fractions and decimals include misalignment, incorrect simplification, and arithmetic errors. Always double-check your steps and results carefully.