Addition Lesson: Strategies, Techniques, and Practical Applications

Lesson Overview

• What Is Addition?
• What Are the Important Addition Rules?
• How Do You Add Fractions?
• How Do You Add Decimals?
• How Do You Add Powers?
• How Do You Add Reciprocal Numbers?
• Conclusion

Addition is one of the fundamental operations in mathematics, serving as the building block for more complex concepts in arithmetic and beyond. In this lesson, you will explore various strategies and techniques for performing addition, from basic counting and number line methods to mental math tricks and column addition. You'll also learn how to apply these techniques to real-life situations such as budgeting, measuring, and problem-solving.

What Is Addition?

Addition is a basic arithmetic operation that involves combining two or more numbers to find their total or sum. It answers the question, "How many in all?" or "What is the total amount?" The numbers being added are called addends, and the result is called the sum.

Example:

• If you add 4 and 3:
  4 + 3 = 7
  Here, 4 and 3 are addends, and 7 is the sum.

Key Features of Addition:

Identity Property: Adding zero to a number doesn't change its value.
Example: 8 + 0 = 8

Commutative Property: Changing the order of addends doesn't change the sum.
Example: 5 + 2 = 2 + 5 = 7

Associative Property: Grouping of numbers doesn't affect the result.
Example: (1 + 2) + 3 = 1 + (2 + 3) = 6

What Are the Important Addition Rules?

Addition follows a set of fundamental mathematical rules that make calculations consistent, logical, and easy to understand. These rules apply across number types and help simplify problem-solving in both basic arithmetic and advanced mathematics.

1. Commutative Property of Addition

The order of addends does not affect the sum.
Rule:
If a and b are numbers, then:
a + b = b + a
Example: 7 + 5 = 5 + 7 = 12

2. Associative Property of Addition

Grouping of addends does not affect the sum.
Rule:
If a, b, and c are numbers, then:
(a + b) + c = a + (b + c)
Example: (2 + 3) + 4 = 2 + (3 + 4) = 9

3. Identity Property of Addition

Adding zero to a number does not change its value.
Rule:
a + 0 = a
Example: 9 + 0 = 9

4. Addition of Negative Numbers (Integers)

When adding negative numbers, move left on the number line.
Rules:

• Positive + Negative = Subtract and keep the sign of the larger number.
• Negative + Negative = Add absolute values and keep the negative sign.
  Examples:
• 5 + (–3) = 2
• –4 + (–6) = –10

5. Decimal Addition Rule

Align the decimal points before adding.
Example:
2.50
+1.75
=4.25

6. Fraction Addition Rule

• If denominators are the same: add numerators.
• If different: find the Least Common Denominator (LCD) first.
  Example:
• ⅔ + ⅓ = (2 + 1)/3 = 3/3 = 1
• ½ + ¼ = (2/4 + 1/4) = 3/4

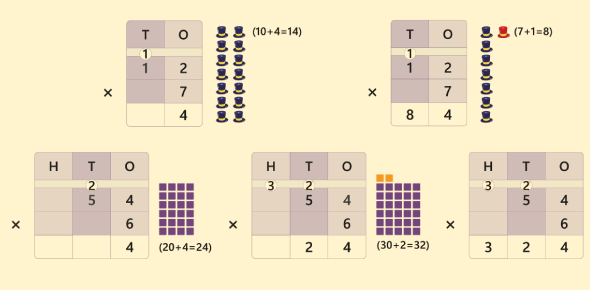
7. Carry-Over Rule in Column Addition

When a sum in any column is 10 or more, write the unit digit and carry the tens digit to the next column.
Example:
57

• 68
  = 125 (carry 1 from 7+8 to next column)

Take These Quizzes

Simple Addition Quiz for Kids: Trivia

Addition Quiz: Practice Test for Beginners! Basic Math

Addition Mixed 5 Min Test

How Do You Add Fractions?

Rule:

• If denominators are the same:
  (a⁄b) + (c⁄b) = (a + c)⁄b
• If denominators are different:
  Find the Least Common Denominator (LCD), convert both fractions, then add.

Example:

• (2⁄5) + (1⁄5) = 3⁄5
• (1⁄3) + (1⁄4) = (4⁄12) + (3⁄12) = 7⁄12

How Do You Add Decimals?

Rule:

• Align decimal points and add digit by digit.

Example:

• 4.26 + 3.10 = 7.36
• 5.8 + 2.35 = 8.15

How Do You Add Powers?

Rule:

• You cannot directly add aˣ + aʸ unless x = y.
• Treat identical powers as like terms:
  aˣ + aˣ = 2aˣ
• Otherwise, evaluate powers before adding.

Example:

• 2³ + 2³ = 8 + 8 = 16
• x² + x² = 2x²

Take These Quizzes

Addition Test: A Quiz to Test your Math Skills!

Addition Timed by 0

Ultimate Quiz on Basic Addition and Regrouping!

How Do You Add Reciprocal Numbers?

Rule:

• Reciprocal of x is 1⁄x.
• Add reciprocals like regular fractions using LCD.

Example:

• (1⁄2) + (1⁄3) = (3⁄6) + (2⁄6) = 5⁄6
• (1⁄4) + (1⁄5) = (5 + 4)⁄20 = 9⁄20

Take These Quizzes

Mathematics for Kids- Addition of Ten Quiz

How Well Do You Know Arithmetic Operations?

Addition Trivia Quiz: Math Skills Test For Beginners!

Conclusion

Great job on completing this addition lesson! You've now gained a comprehensive understanding of addition, one of the most essential mathematical operations. This lesson has taken you through the key concepts of addition, from the basics of combining numbers to more advanced techniques like adding fractions, decimals, and powers.