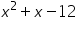Terms Of Factoring Trinomials
-
Factor: x2 + 8x + 15
-
(x + 5)(x + 3)
-
(x - 5)(x - 3)
-
(x + 15)(x + 1)
-
(x + 5)(x - 3)
-
This quiz focuses on factoring trinomials, a fundamental algebraic skill. It assesses the ability to factor quadratic expressions into binomials, enhancing problem-solving skills relevant for academic progression in mathematics.

Quiz Preview
- 2.
Factor: x2 + 3x - 10
-
(x + 2)(x + 5)
-
(x + 5)(x - 2)
-
(x - 5)(x - 2)
-
(x - 5)(x + 2)
Correct Answer
A. (x + 5)(x - 2)Explanation
The given expression is a quadratic trinomial in the form of ax^2 + bx + c. To factorize it, we need to find two binomials whose product equals the given expression. In this case, the binomials are (x + 5) and (x - 2). When we multiply these binomials using the distributive property, we get x^2 + 3x - 10, which is the same as the given expression. Therefore, the correct answer is (x + 5)(x - 2).Rate this question:
-
- 3.
Factor the trinomial below x2 +7x + 6
-
-6 and -1
-
(x + 6)(x + 1)
-
(x - 6)(x - 1)
-
(x + 2)(x + 3)
Correct Answer
A. (x + 6)(x + 1)Explanation
The given trinomial x^2 + 7x + 6 can be factored by finding two numbers that multiply to give 6 and add up to 7. The numbers -6 and -1 satisfy these conditions. Therefore, the factored form of the trinomial is (x + 6)(x + 1).Rate this question:
-
- 4.
X2 – 6x + 8
-
(x – 4)(x + 2)
-
(x + 4)(x + 2)
-
(x – 4)(x – 2)
Correct Answer
A. (x – 4)(x – 2)Explanation
The given expression can be factored as (x - 4)(x - 2) because when the expression is multiplied out, it results in x2 - 6x + 8. The first term in each factor is obtained by multiplying the x term in each factor, and the constant term in each factor (4 and 2) is obtained by multiplying the constant terms in each factor. The middle term in the expression (-6x) is obtained by multiplying the outer and inner terms in the factors (-4x and -2x), which gives -4x - 2x = -6x. Therefore, (x - 4)(x - 2) is the correct factorization.Rate this question:
-
- 5.
Factor: x2 - 8x + 15
-
(x - 3)(x - 5)
-
(x + 3)(x + 5)
-
(x - 3)(x + 5)
-
(x + 3)(x - 5)
Correct Answer
A. (x - 3)(x - 5)Explanation
The given expression is a quadratic trinomial in the form of ax^2 + bx + c. To factorize it, we need to find two numbers whose sum is equal to the coefficient of the middle term (-8) and whose product is equal to the constant term (15). The numbers that satisfy these conditions are -3 and -5. Therefore, the correct answer is (x - 3)(x - 5) since it represents the factored form of the given expression.Rate this question:
-
- 6.
X2 + x – 90
-
(x – 9)(x – 10)
-
(x – 9)(x + 10)
-
(x + 9)(x – 10)
Correct Answer
A. (x – 9)(x + 10)Explanation
The given expression is a quadratic trinomial that can be factored using the difference of squares formula. The correct answer, (x – 9)(x + 10), is obtained by multiplying the factors (x – 9) and (x + 10) together. This can be done by using the distributive property, which states that for any real numbers a, b, and c, a(b + c) = ab + ac. So, multiplying (x – 9) and (x + 10) gives x^2 + 10x - 9x - 90, which simplifies to x^2 + x - 90, the original expression.Rate this question:
-
- 7.
X2 - x - 2
-
(x - 1)(x - 2)
-
(x + 3)(x - 1)
-
(x - 2)(x + 1)
-
(x + 1)(x - 3)
Correct Answer
A. (x - 2)(x + 1)Explanation
The given expression can be factored as (x - 2)(x + 1). This can be determined by using the distributive property to expand (x - 2)(x + 1) and simplifying the terms. The resulting expression is x^2 - x - 2, which matches the given expression. Therefore, (x - 2)(x + 1) is the correct answer.Rate this question:
-
- 8.
Factor: x2 - 4x - 12
-
(x + 4)(x - 3)
-
(x - 4)(x + 3)
-
(x + 6)(x - 2)
-
(x - 6)(x + 2)
Correct Answer
A. (x - 6)(x + 2)Explanation
The given expression is a quadratic trinomial in the form of x^2 - 4x - 12. To factorize it, we need to find two numbers that multiply to give -12 and add up to -4. The numbers -6 and 2 satisfy these conditions because (-6)(2) = -12 and (-6) + 2 = -4. Therefore, the correct answer is (x - 6)(x + 2).Rate this question:
-
- 9.
2x2 + 2x – 4
-
2(x – 1)(x + 2)
-
2(x + 1)(x + 2)
-
(2x – 1)(x + 4)
Correct Answer
A. 2(x – 1)(x + 2)Explanation
The given expression is a quadratic trinomial. To factorize it, we can look for two binomials that multiply to give the trinomial. In this case, the binomials are (x - 1) and (x + 2). Multiplying these binomials together gives us 2(x - 1)(x + 2), which is the correct answer.Rate this question:
-
- 10.
Factor the trinomial
Correct Answer
(x + 4) (x - 3)
(x+4)(x-3)
(x+ 4)(x- 3)
(x +4)(x -3)Explanation
This is a trinomial. We want to multiply to -12 and add to a positive 1. Therefore we need +4 and -3.Rate this question:
Quiz Review Timeline (Updated): Nov 24, 2023 +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Nov 24, 2023Quiz Edited by
ProProfs Editorial Team -
Mar 02, 2015Quiz Created by
Philip Benanti
8-5 Factoring Trinomials When A = 1
This quiz tests the ability to factor trinomials with a leading coefficient of 1. It includes questions on identifying binomial factors and determining rectangle dimensions from a...
Questions:
5 |
Attempts:
903 |
Last updated:
Mar 21, 2023
|
Algebra 1B: Unit 11: Obj 5: QUIZ
This Algebra 1B: Unit 11: Obj 5 quiz assesses the ability to factor trinomials. Participants are required to solve problems such as factoring trinomials into binomial products,...
Questions:
10 |
Attempts:
102 |
Last updated:
Mar 15, 2023
|
Algebra 1B: Unit 11 Obj 5: Factoring Trinomials
This Algebra 1B quiz focuses on factoring trinomials, assessing the learner's ability to factor quadratic expressions of the form x2 + bx + c. It includes problems like x2 + 8x +...
Questions:
7 |
Attempts:
66 |
Last updated:
Jun 21, 2023
|
Can You Pass This Factoring Trinomials Test?
Factoring is a mathematical operation which used to separate down the numbers that multiply together to form another number. Factoring trinomials mean finding two...
Questions:
10 |
Attempts:
1240 |
Last updated:
Sep 25, 2024
|
8-5 Factoring Trinomials When A = 1
This quiz tests the ability to factor trinomials with a leading coefficient of 1. It includes questions on identifying binomial factors and determining rectangle dimensions from a...
Questions:
5 |
Attempts:
903 |
Last updated:
Mar 21, 2023
|
Algebra 1B: Unit 11: Obj 5: QUIZ
This Algebra 1B: Unit 11: Obj 5 quiz assesses the ability to factor trinomials. Participants are required to solve problems such as factoring trinomials into binomial products,...
Questions:
10 |
Attempts:
102 |
Last updated:
Mar 15, 2023
|
 Back to top
Back to top