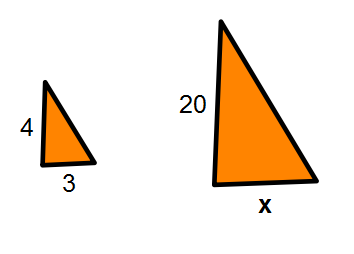5.2 Similar Triangles- You Will Need The Paper Assignment To Complete IT Online.

Reviewed by Editorial Team
The ProProfs editorial team is comprised of experienced subject matter experts. They've collectively created over 10,000 quizzes and lessons, serving over 100 million users. Our team includes in-house content moderators and subject matter experts, as well as a global network of rigorously trained contributors. All adhere to our comprehensive editorial guidelines, ensuring the delivery of high-quality content.
Learn about Our Editorial Process
| By Blinda Windham
B
Blinda Windham
Community Contributor
Quizzes Created: 9 | Total Attempts: 1,833
| Attempts: 196
SettingsSettings
Please wait...
  • 1/11 Questions

    Problem 2.  Are the two figures similar?  If so what is the similarity statement.  Check 2 of the following choices.

    • Similar
    • Not similar
    • Triangle CBA is similar to Triangle FGH
    • Triangle CBA is similar to Triangle GFH
Please wait...
About This Quiz

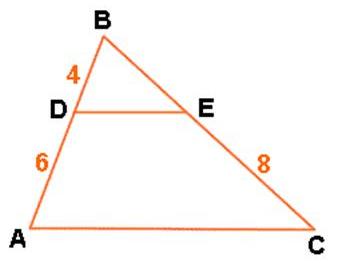
Determing if two figures are similar by using ratios and proportions. When the figures are similar state the similarity statement.

Similarity Quizzes & Trivia

Quiz Preview

  • 2. 

    Problem 4.  The triangles are similar, complete the similarity statement. Triangle JKL is similar to Triangle _______.

    • Triangle TUV

    • Triangle UTV

    • Triangle VUT

    Correct Answer
    A. Triangle TUV
    Explanation
    The similarity statement for the given triangles is Triangle JKL is similar to Triangle TUV. This is because the order of the vertices in the similarity statement must match the order of the corresponding vertices in the triangles. In this case, J corresponds to T, K corresponds to U, and L corresponds to V. Therefore, the correct similarity statement is Triangle JKL is similar to Triangle TUV.

    Rate this question:

  • 3. 

    Porblem 6.  True or False.  Are the triangles similar?

    • True

    • False

    Correct Answer
    A. False
    Explanation
    The question asks whether the triangles are similar. Similar triangles have the same shape but may have different sizes. To determine if two triangles are similar, we need to compare their corresponding angles and side lengths. However, the question does not provide any information about the triangles or their properties. Therefore, we cannot determine if the triangles are similar or not based on the given information.

    Rate this question:

  • 4. 

    Problem 7.  The two triangle are similar.  Complete the similarity statement. Triangle TUV is similar to Triangle ______.

    • QSR

    • QRS

    • RQS

    Correct Answer
    A. QRS
    Explanation
    The similarity statement for two triangles states that their corresponding angles are congruent and their corresponding sides are proportional. In this case, the given triangles TUV and QRS are similar because they have corresponding angles that are congruent. Therefore, the correct similarity statement is "Triangle TUV is similar to Triangle QRS."

    Rate this question:

  • 5. 

    Problem 10.  Is Triangle FGH similar to Triangle VUW?

    • True

    • False

    Correct Answer
    A. False
    Explanation
    In order for two triangles to be similar, their corresponding angles must be congruent and their corresponding sides must be proportional. Without any additional information or given measurements, it is not possible to determine if Triangle FGH is similar to Triangle VUW. Therefore, the correct answer is False.

    Rate this question:

  • 6. 

    Problem 11.  What is the length of FS and FR?

    • FS=32 and FR=52

    • FS=56 and FR=91

    • FS=52 and FR=32

    Correct Answer
    A. FS=32 and FR=52
    Explanation
    The given answer states that FS has a length of 32 and FR has a length of 52. This means that FS is shorter than FR.

    Rate this question:

  • 7. 

    Problem 13.   In triangle LJK, LJ=28, KJ=x.  In triangle RPQ, RP=42, PQ=33.  The two triangles are similar.  What is the value of x?

    • 11

    • 22

    • 33

    Correct Answer
    A. 22
    Explanation
    Since the two triangles are similar, their corresponding sides are proportional. In triangle LJK, LJ=28 and KJ=x. In triangle RPQ, RP=42 and PQ=33. We can set up a proportion to find the value of x:

    LJ/KJ = RP/PQ

    28/x = 42/33

    Cross multiplying, we have:

    33 * 28 = 42 * x

    924 = 42x

    Dividing both sides by 42, we find:

    x = 924/42 = 22

    Therefore, the value of x is 22.

    Rate this question:

  • 8. 

    Problem 14.  TriangleTUV is similar to Triangle MLK.  UV = 60, KL = 130 and LM = 117.  What is the length of UT?

    • 66.67

    • 62

    • 54

    Correct Answer
    A. 54
    Explanation
    Since Triangle TUV is similar to Triangle MLK, we can use the property of similar triangles that states corresponding sides are proportional. Therefore, we can set up the following proportion:

    UT/ML = UV/KL

    Substituting the given values, we have:

    UT/117 = 60/130

    Cross-multiplying and solving for UT, we get:

    UT = (117 * 60) / 130 = 54

    Rate this question:

  • 9. 

    Problem 16.  Triangle VPW is similar to Triangle QPR.  PV = 9, PQ = 18, and PR = 22, what is the length of PW?

    • 11

    • 9

    • 6

    Correct Answer
    A. 11
    Explanation
    Since triangle VPW is similar to triangle QPR, we can set up a proportion using the corresponding sides. The length of PV is 9 and the length of PQ is 18. The length of PW is unknown, and the length of PR is 22. Setting up the proportion, we have PW/PR = VP/PQ. Plugging in the given values, we get PW/22 = 9/18. Simplifying the proportion, we have PW/22 = 1/2. Cross multiplying, we get PW = 22/2 = 11. Therefore, the length of PW is 11.

    Rate this question:

  • 10. 

    Problem 18.  Triangle ABC is similar to Triangle FED.  AB = 77, BC = 11x + 11, FE = 21 and DE = 30, what is the value of x?

    • 12

    • 9

    • 2.5

    Correct Answer
    A. 9
    Explanation
    Since Triangle ABC is similar to Triangle FED, the corresponding sides are proportional. We can set up the proportion AB/FE = BC/DE. Plugging in the given values, we get 77/21 = (11x + 11)/30. Cross multiplying and solving for x, we find that x = 9.

    Rate this question:

  • 11. 

    Problem 19.  Triangle JUT is similar to Triangle JKL.  JU = (-4+4x), JK = 64, JT=27 and JL = 72.  What is the value of x?

    • 7

    • 11

    • 24

    Correct Answer
    A. 7
    Explanation
    Triangle JUT is similar to triangle JKL, which means that their corresponding angles are equal and their corresponding sides are proportional. In this case, we are given that JU = -4 + 4x and JK = 64. We also know that JT = 27 and JL = 72.

    To find the value of x, we can set up a proportion using the corresponding sides of the triangles:

    (JU / JK) = (JT / JL)

    ((-4 + 4x) / 64) = (27 / 72)

    Cross multiplying and simplifying the equation, we get:

    72(-4 + 4x) = 64(27)

    -288 + 288x = 1728

    288x = 2016

    x = 7

    Therefore, the value of x is 7.

    Rate this question:

Quiz Review Timeline (Updated): Mar 15, 2023 +

Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.

  • Current Version
  • Mar 15, 2023
    Quiz Edited by
    ProProfs Editorial Team
  • Nov 11, 2012
    Quiz Created by
    Blinda Windham
Back to Top Back to top
Advertisement
×

Wait!
Here's an interesting quiz for you.

We have other quizzes matching your interest.