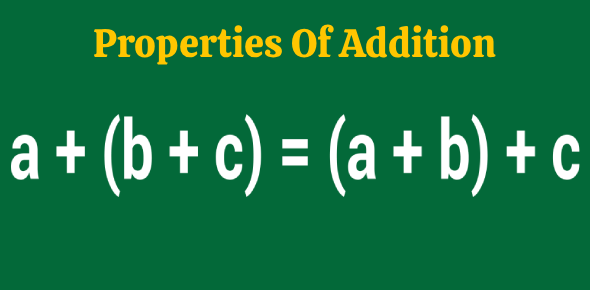Addition and Multiplication: Core Properties, Rules, and Everyday Uses
Lesson Overview
- The Commutative Property of Addition
- The Commutative Property of Multiplication
- Why Subtraction and Division Are NOT Commutative
- The Associative Property of Addition
- The Associative Property of Multiplication
- Why Subtraction and Division Are NOT Associative
- Using Properties to Solve Problems Faster
- Identifying the Property in a Math Sentence
- Properties Work with All Numbers
Mathematics has many tools and rules that make solving problems faster and smarter. Two important math operations-addition and multiplication-follow special rules called properties. These properties help you solve problems more easily, check your work, and understand how numbers behave.
In this lesson, we'll explore:
- The commutative and associative properties
- How these properties work for both addition and multiplication
- Why subtraction and division don't follow the same rules
- How to use these properties in solving problems and identifying patterns
By the end of this lesson, you'll not only know the rules-you'll be able to use them confidently in your math work.
The Commutative Property of Addition
The commutative property tells us that when adding numbers, the order does not matter-the result stays the same.
Rule:
a + b = b + a
This means that if you're adding two numbers, you can swap them around, and the sum remains the same.
Examples:
- 6 + 4 = 10
- 4 + 6 = 10
→ The sum is still 10 - 10 + 25 = 35
- 25 + 10 = 35
→ Still 35
Why It Helps:
This property makes it easier to solve problems mentally. If one way is harder, you can rearrange the numbers to make the calculation simpler. For example, it may be easier to add 10 + 25 than 25 + 10 in your head because 10 is a friendly number.
The Commutative Property of Multiplication
This property works the same way for multiplication-you can change the order of the numbers and the product stays the same.
Rule:
a × b = b × a
This is helpful when you're solving multiplication problems with numbers you're more comfortable with in a certain order.
Examples:
- 3 × 7 = 21
- 7 × 3 = 21
→ Both are 21 - 12 × 5 = 60
- 5 × 12 = 60
→ Still 60
Helpful Tip:
This means you don't need to memorize both 3 × 7 and 7 × 3-you only need to learn one fact!
Why Subtraction and Division Are NOT Commutative
Now let's look at subtraction and division. These operations do not follow the commutative property. The order does matter here.
Examples (Subtraction):
- 9 − 5 = 4
- 5 − 9 = −4 → Not the same
So: 9 − 5 ≠ 5 − 9
Examples (Division):
- 12 ÷ 3 = 4
- 3 ÷ 12 = 0.25 → Not the same
So: 12 ÷ 3 ≠ 3 ÷ 12
What This Means:
You can't swap the numbers when subtracting or dividing. You must keep them in the correct order to get the correct answer.
The Associative Property of Addition
The associative property is all about grouping. It says that when you add three or more numbers, it doesn't matter how you group them-the sum is the same.
Grouping is shown with parentheses ( ).
Rule:
(a + b) + c = a + (b + c)
This means you can add the first two numbers, or the last two, and still get the same result.
Examples:
- (2 + 3) + 5 = 5 + 5 = 10
- 2 + (3 + 5) = 2 + 8 = 10
→ Both give 10 - (7 + 4) + 9 = 11 + 9 = 20
- 7 + (4 + 9) = 7 + 13 = 20
→ Still 20
Why It Helps:
If two numbers are easier to add together, group them first-even if they are not written next to each other.
The Associative Property of Multiplication
Just like with addition, the associative property works for multiplication too. When multiplying three or more numbers, it doesn't matter which ones you multiply first.
Rule:
(a × b) × c = a × (b × c)
You can group the numbers any way, and the product will be the same.
Examples:
- (2 × 3) × 4 = 6 × 4 = 24
- 2 × (3 × 4) = 2 × 12 = 24
→ Both give 24 - (5 × 2) × 6 = 10 × 6 = 60
- 5 × (2 × 6) = 5 × 12 = 60
→ Still 60
Helpful Tip:
Grouping helps make multiplication easier when two numbers are friendlier to multiply.
Why Subtraction and Division Are NOT Associative
Like with the commutative property, subtraction and division do not follow the associative property.
Changing the grouping changes the answer.
Subtraction Example:
- (10 − 4) − 2 = 6 − 2 = 4
- 10 − (4 − 2) = 10 − 2 = 8
→ Different answers
Division Example:
- (20 ÷ 5) ÷ 2 = 4 ÷ 2 = 2
- 20 ÷ (5 ÷ 2) = 20 ÷ 2.5 = 8
→ Not the same
Why It Matters:
For subtraction and division, always do operations in the correct order and grouping.
Using Properties to Solve Problems Faster
Understanding these properties helps you solve problems more quickly by rearranging or grouping numbers in smarter ways.
Example 1:
Instead of 27 + 3 + 13, group 27 + 13 first:
27 + 13 = 40
40 + 3 = 43
Example 2:
To solve 4 × 25 × 2
Group 25 × 4 = 100
Then 100 × 2 = 200
Changing the order or grouping using these properties can make solving much faster and simpler.
Identifying the Property in a Math Sentence
Math problems often ask you to say which property is being used in a sentence.
Example 1:
6 + 9 = 9 + 6
→ Order changed → Commutative Property of Addition
Example 2:
(2 × 3) × 5 = 2 × (3 × 5)
→ Grouping changed → Associative Property of Multiplication
Tip:
- Look for change in order → commutative
- Look for change in grouping → associative
Properties Work with All Numbers
These properties work with small and large numbers, even with:
- Odd or even numbers
- Zero or one
- Any whole numbers
Example:
Even with 0:
3 + 0 = 0 + 3 → Commutative Property of Addition
Even with 1:
1 × 6 = 6 × 1 → Commutative Property of Multiplication
The properties are always true as long as the operation is addition or multiplication.
Rate this lesson:
 Back to top
Back to top