Fraction Word Problems: Techniques, Solutions, and Uses

Lesson Overview

• What Are Fractions?
• What Techniques Are Effective in Solving Fraction Word Problems?
• How Do We Accurately Add and Subtract Fractions?
• Why Is Understanding Equivalent Fractions Essential?
• How Do We Solve Fraction Word Problems Involving Multiplication and Division?
• How Can Fraction Word Problems Develop Critical Thinking?
• Practice Problems for Mastery
• Avoiding Common Fraction Word Problem Mistakes

Have you ever tried sharing a pizza evenly with friends and found yourself unsure how to slice it fairly? Fraction word problems often appear daunting, especially when they reflect real-world scenarios like sharing food, dividing materials, or calculating time. This lesson on Fraction Word Problems resolves such confusion, enhancing your ability to apply mathematical concepts practically and confidently.

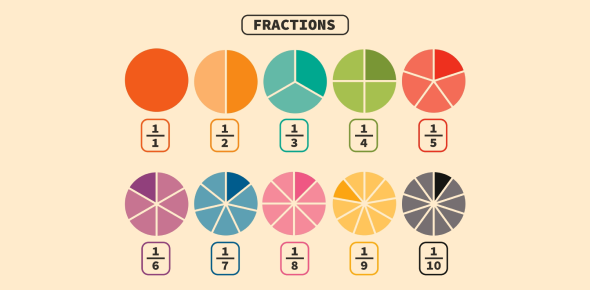
What Are Fractions?

Fractions represent parts of a whole or parts of a group. They indicate that a whole object or group has been divided into equal parts. A fraction consists of two numbers separated by a horizontal or diagonal line:

• Numerator (top number): indicates how many parts you have or are focusing on.
  
• Denominator (bottom number): tells you how many equal parts the whole is divided into.
  

Example:

If you slice a pizza into 8 equal slices and eat 3 slices, you've eaten 3 out of 8, or 3/8 of the pizza.

3/8

Types:

• Proper fraction: 2/5
  
• Improper fraction: 7/4
  
• Mixed number: 1 3/4

Take This Quiz!

Fraction Math Quiz

What Techniques Are Effective in Solving Fraction Word Problems?

Discover proven strategies that simplify fraction word problems. Learning these techniques aids in clearly understanding problems, organizing information, and arriving at correct solutions.

Systematic Approach

Following a systematic approach simplifies complex word problems:

1. Read Thoroughly: Understand the scenario and what the problem asks.
2. Identify Key Information: Highlight critical numerical data and keywords.
3. Decide on Operations: Determine whether to add, subtract, multiply, or divide fractions.
4. Solve Methodically: Execute calculations step by step.
5. Review Answers: Verify solutions to ensure accuracy.

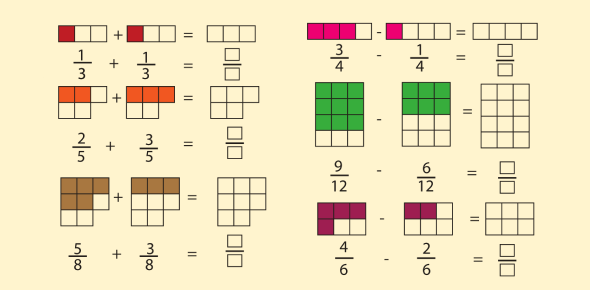
How Do We Accurately Add and Subtract Fractions?

Explore detailed methodologies for adding and subtracting fractions, essential for solving complex fraction word problems involving combined or leftover quantities.

Adding Fractions

When adding fractions, convert them to have common denominators:

• Identify the least common denominator (LCD).
• Convert each fraction.
• Add numerators while keeping the denominator.
• Simplify the result if necessary.

Example: 1/2 + 1/6

• LCD is 6.
• Convert 1/2 to 3/6.
• Add 3/6 + 1/6 = 4/6 = 2/3 after simplifying.

Subtracting Fractions

Similarly, subtraction requires common denominators:

• Identify the LCD.
• Convert each fraction.
• Subtract numerators while keeping the denominator.
• Simplify if possible.

Example: 1 - (1/4 + 1/8)

• LCD is 8.
• Convert fractions: 1/4 = 2/8.
• Add first: 2/8 + 1/8 = 3/8.
• Subtract from whole: 8/8 - 3/8 = 5/8.

Why Is Understanding Equivalent Fractions Essential?

Understanding equivalent fractions is fundamental because it simplifies calculations, ensuring accuracy when solving fraction word problems involving comparison or simplification.

Equivalent fractions represent the same value despite having different numerators and denominators. Recognizing and creating equivalent fractions aids in comparisons, additions, subtractions, and problem-solving clarity.

Generating Equivalent Fractions

• Multiply or divide the numerator and denominator by the same non-zero number.
• Example: 2/4 = 1/2, 3/6 = 1/2, ensuring accurate computations.

How Do We Solve Fraction Word Problems Involving Multiplication and Division?

Multiplication and division are common operations in fraction word problems involving repeated quantities or dividing items among groups. Understanding these operations provides accurate solutions.

Multiplying Fractions

• Multiply numerators together and denominators together.
• Simplify the resulting fraction.

Example: 1 1/2 × 3

• Convert mixed number: 1 1/2 = 3/2.
• Multiply: (3/2) × 3 = 9/2 = 4 1/2.

Dividing Fractions

• Invert (flip) the second fraction.
• Multiply the first fraction by the inverted second fraction.

Example: 3/4 ÷ 1/8

• Invert second fraction: 8/1.
• Multiply: (3/4) × (8/1) = 24/4 = 6.

How Can Fraction Word Problems Develop Critical Thinking?

Fraction word problems cultivate critical thinking by challenging you to interpret scenarios, analyze information, select appropriate mathematical operations, and justify solutions logically.

Engaging with Problems

• Ask yourself what information is crucial.
• Determine how different pieces of information relate.
• Evaluate multiple solving methods for accuracy.

Practice Problems for Mastery

Solving various practice problems reinforces concepts, builds confidence, and prepares for assessments and real-world applications. Below are practice problems with detailed solutions for self-assessment.

1. Fraction Addition: Anna used 3/4 cups of flour and then another 1/8 cup. How much flour did she use altogether?
2. Fraction Subtraction: After jogging 7/8 of a mile, Mark rested. Later he completed his 1-mile run. How much distance did Mark cover after resting?
3. Multiplying Fractions: A recipe calls for 2/3 cup of milk per serving. How much milk is required for 4 servings?
4. Dividing Fractions: If you have 5/6 of a yard of fabric and need strips measuring 1/3 of a yard, how many strips can you cut?

Avoiding Common Fraction Word Problem Mistakes

Common mistakes in fraction word problems include:

• Forgetting to simplify fractions.
• Misidentifying operations from context.
• Incorrectly finding common denominators.

Being mindful of these errors helps maintain accuracy in solving fraction word problems effectively.

Take This Quiz!

I - Fraction Word Problems