Area of a Triangle: Formula, Calculation Steps, and Example Problems
Lesson Overview
Learning how to calculate the area of a triangle is an essential geometry skill. The area tells us how much space is inside the triangle, and understanding this concept lays the foundation for more advanced math and science topics.
Area plays an important role in both academic study and everyday life. From estimating the space of a triangular garden to designing road signs, being able to calculate area helps make informed decisions. This lesson will explore what triangles are, how we measure their area, and why the formula we use works. Through step-by-step examples and a clear breakdown of concepts, this guide will build a solid understanding of how to work with triangle areas confidently.
What Is a Triangle?
A triangle is a two-dimensional shape that has exactly three sides and three angles. It is the simplest of all polygons, yet it plays a crucial role in geometry due to its strength, symmetry, and versatility.
The sides of a triangle can be of equal or unequal lengths. The angles inside a triangle always add up to 180 degrees, regardless of the triangle's size or shape. Understanding the basic properties of triangles is essential before learning how to calculate their area.
Here are the main types of triangles:
- Equilateral Triangle: All three sides are equal in length and all angles are 60 degrees.
- Isosceles Triangle: Two sides are equal in length, and the angles opposite those sides are equal.
- Scalene Triangle: All three sides and all three angles are different.
- Right Triangle: One of the angles is exactly 90 degrees.
Each of these triangle types follows the same formula for area. However, identifying the base and height accurately is key to using the formula correctly.
Understanding Base and Height
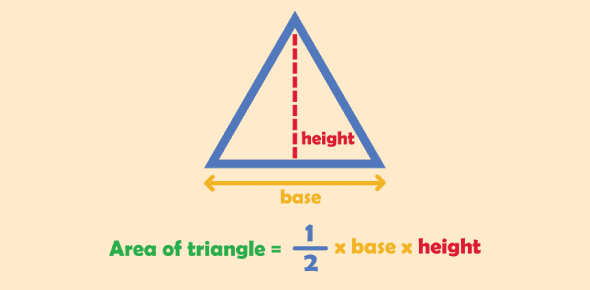
To calculate the area of a triangle, two specific measurements are needed: the base and the height. These parts must be clearly defined and correctly identified for the area formula to work.
- Base (b): The base is usually one of the sides of the triangle and is often the one drawn horizontally at the bottom. Any of the three sides can serve as the base, depending on how the triangle is positioned.
- Height (h): The height (or altitude) is the perpendicular distance from the base to the opposite vertex. It must form a right angle (90 degrees) with the base. The height is not always inside the triangle-it can fall outside if the triangle is obtuse.
Understanding how base and height relate is crucial because they must be perpendicular to each other. If the height is measured incorrectly, the area will also be incorrect.
Formula for the Area of a Triangle
Once the base and height are identified, the formula for the area of a triangle is simple and consistent:
Area = (base × height) / 2
This formula works for all types of triangles as long as the base and height are perpendicular to each other.
Why divide by 2?
When you take a parallelogram and draw a diagonal from one corner to the opposite corner, you divide it into two identical triangles. Since the area of a parallelogram is base × height, the area of each triangle is half that amount. That's why we divide by two in the triangle formula.
This formula provides a straightforward way to calculate the amount of space inside any triangle, whether it's equilateral, scalene, or right-angled.
Step-by-Step Examples
Let's look at some worked-out examples that follow the area formula. These examples demonstrate how to plug in values and simplify the expression.
Example 1:
A triangle has a base of 10 cm and a height of 25 cm. What is its area?
Step 1: Multiply the base and the height: 10 × 25 = 250
Step 2: Divide by 2: 250 ÷ 2 = 125 cm²
Example 2:
A triangle has a base of 4 inches and a height of 6 inches. What is its area?
Step 1: Multiply the base and height: 4 × 6 = 24
Step 2: Divide by 2: 24 ÷ 2 = 12 in²
Example 3:
A triangle has a base of 30 feet and a height of 25 feet. What is its area?
Step 1: Multiply 30 × 25 = 750
Step 2: Divide 750 ÷ 2 = 375 ft²
These examples show how the process remains the same regardless of the units or the size of the triangle.
Solving for Missing Base or Height
Sometimes, instead of finding the area, you are given the area and asked to find the missing base or height. This means you'll need to use algebra and rearrange the formula:
Original formula: Area = (base × height) / 2
To solve for base: base = (2 × area) / height
To solve for height: height = (2 × area) / base
Example:
A triangle has an area of 40 cm² and a height of 5 cm. What is the base? Step 1: Multiply area by 2: 40 × 2 = 80
Step 2: Divide by the height: 80 ÷ 5 = 16 cm
Another example:
A triangle has an area of 54 in² and a base of 9 inches. What is the height? Step 1: Multiply area by 2: 54 × 2 = 108
Step 2: Divide by base: 108 ÷ 9 = 12 inches
This skill is especially useful in solving word problems or working with missing dimensions in geometric shapes.
Relationship Between Triangles and Parallelograms
There is a strong connection between triangles and parallelograms. Understanding this relationship helps explain the logic behind the triangle area formula.
A parallelogram is a four-sided shape with opposite sides that are equal and parallel. If you draw a diagonal from one corner to the opposite, you split the parallelogram into two congruent triangles. This geometric property shows that each triangle is exactly half of the whole parallelogram.
Parallelogram Formula:
- Area = base × height
Triangle Formula:
- Area = (base × height) / 2
This means the triangle shares the same base and height as the parallelogram, but only occupies half the space. This concept also helps when working with complex figures where shapes are combined-like dividing irregular figures into simpler triangles and parallelograms to find the total area.
Recognizing how triangles and parallelograms relate builds a deeper understanding of geometry and supports spatial reasoning. It also provides a practical way to estimate or calculate area in architectural design, art, and engineering.
Take This Quiz:
Rate this lesson:
 Back to top
Back to top