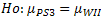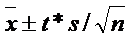Test3 Confidence Interval And Hypothesis Testing

Sample exam for testing knowledge of Confidence Interval, Hypothesis Testing.
- 1.
When is a statistical procedure robust?
- A.
When sample is at least 20% of the population?
- B.
When it is used even though the sample is not SRS.
- C.
When confidence level or the P-value does not change very much even when the conditions are not fully met.
- D.
When the correlation between the test statistic and the P-value is close to 1.0 (or the correlation between the level of confidence and z* ic close to 1.).
Correct Answer
C. When confidence level or the P-value does not change very much even when the conditions are not fully met.Explanation
When confidence level or P-value does not change very much even when the conditions are not met. For example, confidence level or P-value using t-distribution is robust because these values do not change very much even if the distribution is not Normal as long as there is no extreme outlier or extreme skewness of the data.Rate this question:
-
- 2.
In order to compare free-throw shooting skills of Deacons versus Teachers, 12 Deacons and 16 Teachers were randomly selected to test the hypotheses: Ho: μD=μT versus Ha: μD<μT . The results of the free-throw shooting skills test are: Two Sample T-test results (without pooled variances): μD=mean of Deacons μT=mean of Teachers Ho: μD-μT = 0 Ha: μD-μT < 0 Difference Sample Mean Std. Err. DF t-stat P-value μD-μT -7.31 4.2917 11 -1.5 0.081 On the basis of the P-value, what should we conclude at α=0.10?
- A.
The mean free-throw score for Teachers equals the mean for Deacons.
- B.
The mean free-throw score for Teachers is significantly less than the mean for Deacons.
- C.
The mean free-throw score for Deacons is significantly less than the mean for Teachers.
- D.
The mean free-throw score for Deacons is not significantly less than the mean for Teachers.
Correct Answer
C. The mean free-throw score for Deacons is significantly less than the mean for Teachers.Explanation
If the P-value < α, Reject Ho or Significant.
If the P-value > α, Fail to Reject Ho or Not Significant.Rate this question:
-
- 3.
Consider an SRS of size 20 from a Normally distributed population, If x-bar=45 and s=15, what is the appropriate formula for a 95% confidence interval for µ?
- A.
X ̅ ± z*σ / √n
- B.
X ̅ ± t*σ ⁄ √n
- C.
x ̅ ± z*s ⁄ √n
- D.
X ̅± t*s ⁄ √n
Correct Answer
D. X ̅± t*s ⁄ √nExplanation
When σ is unknown and the population is Normal and nRate this question:
-
- 4.
Consider an SRS of size 16 from a Normally distributed population with σ=16, If x-bar 12x">=45 and s=12, what is the appropriate formula for a 95% confidence interval for µ?
- A.
x ̅ ± z* σ ⁄ √n
- B.
X ̅ ± z* s ⁄ √n
- C.
x ̅ ± t* σ ⁄ √n
- D.
x ̅ ± t* s ⁄ √n
Correct Answer
A. x ̅ ± z* σ ⁄ √nExplanation
Use z* and σ.Rate this question:
-
- 5.
You want to compare the daily items sold for two game consoles: Playstation3(PS3) and NintendoWII(WII). Over the next 80 days, 40 days are randomly assigned to PS3 and 40 days to WII. At the end, you compute a 95% confidence interval for the difference in mean daily items sold for the two game consoles to be (-20, 10). On the basis of this confidence interval, can you conclude that there is a significant difference between the mean daily items sold for the two game consoles at α=0.05? (i.e., can you reject
- A.
No because the mean daily items sold cannot be negative.
- B.
No, because the interval tells us the mean daily items sold for the two game consoles and doesn’t provide information for comparing them.
- C.
No, because the confidence interval contains zero.
- D.
Yes, because the confidence interval contains zero.
- E.
Yes, because we are 95% confident that the difference between the mean daily items sold for PS3 and WII is somewhere between -20 and 10.
Correct Answer
C. No, because the confidence interval contains zero.Explanation
Using confidence interval to accept or reject Ho:
When the hypothesized value is in the interval then we fail to reject Ho. When it is NOT in the interval, we Reject Ho.
When comparing two means, the hypothesized value is zero.Rate this question:
-
- 6.
You want to compare the daily items sold for two game consoles: Playstation3(PS3) and NintendoWII(WII). Over the next 80 days, 40 days are randomly assigned to PS3 and 40 days to WII. At the end, you compute a 95% confidence interval for the difference in mean daily items sold for the two game consoles to be (-20, -10). On the basis of this confidence interval, can you conclude that there is a significant difference between the mean daily items sold for the two game consoles at α=0.05? (i.e., can you reject
- A.
No because the mean daily items sold cannot be negative.
- B.
No, because the interval tells us the mean daily items sold for the two game consoles and doesn’t provide information for comparing them.
- C.
No, because the confidence interval contains zero.
- D.
Yes, because the confidence interval does not contains zero.
- E.
Yes, because we are 95% confident that the difference between the mean daily items sold for PS3 and WII is somewhere between -20 and 10.
Correct Answer
D. Yes, because the confidence interval does not contains zero.Explanation
Using confidence interval to accept or reject Ho:
When the hypothesized value is in the interval then we fail to reject Ho. When it is NOT in the interval, we Reject Ho.
When comparing two means, the hypothesized value is zero.Rate this question:
-
- 7.
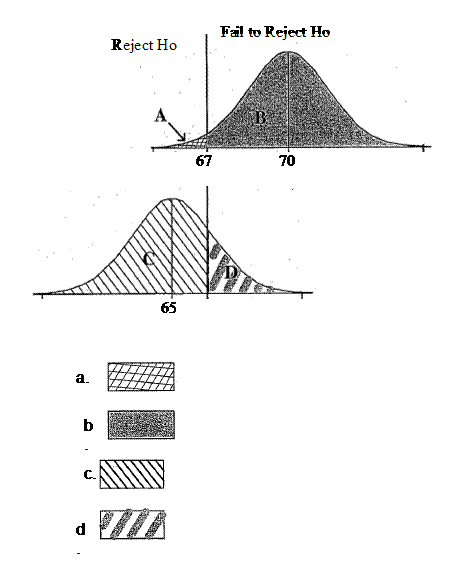
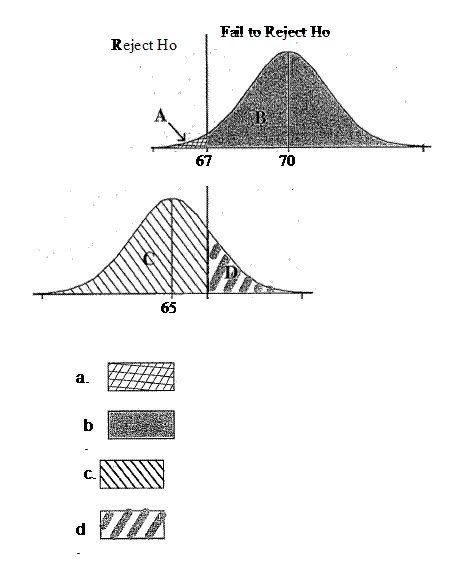
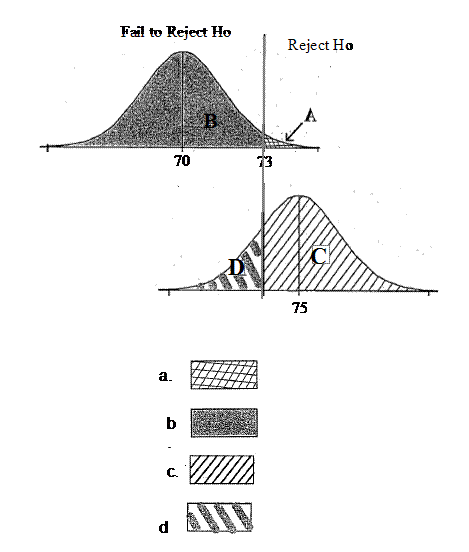
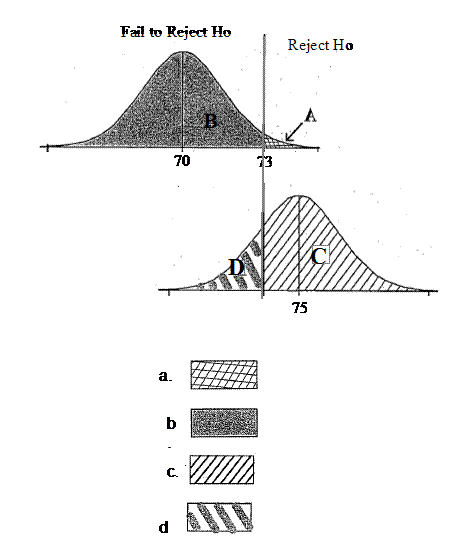
Consider the following sampling distributions. The normal curve on the top represents the sampling distribution for x-bars assuming Ho: µ=70 is true.At a=.05, x-bar values that are less than 67 will lead to the rejection of Ho in favor of Ha: µ < 70The normal curve on the bottom is the sampling distribution for x-bars assuming µ =65.Which area represent the probability of Type II error?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
D. DExplanation
The area represented by choice d represents the probability of Type II error. Type II error occurs when we fail to reject the null hypothesis (Ho) when it is actually false. In this case, the null hypothesis is that the population mean (µ) is equal to 70. The alternative hypothesis (Ha) is that the population mean is less than 70. Therefore, if the true population mean is actually 65 (as represented by the normal curve on the bottom), any x-bar values that fall within the shaded area (choice d) would lead to a Type II error.Rate this question:
-
- 8.
Consider the following sampling distributions. The normal curve on the top represents the sampling distribution for x-bars assuming Ho: µ=70 is true.At a=.05, x-bar values that are less than 67 will lead to the rejection of Ho in favor of Ha: µ < 70The normal curve on the bottom is the sampling distribution for x-bars assuming µ =65.Which area represent the probability of Type I error?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
A. AExplanation
The area represented by option a represents the probability of Type I error. Type I error occurs when the null hypothesis (Ho) is rejected, even though it is true. In this case, the null hypothesis is that µ = 70. If the x-bar values are less than 67, it would lead to the rejection of Ho, indicating a Type I error.Rate this question:
-
- 9.
Consider the following sampling distributions. The normal curve on the top represents the sampling distribution for x-bars assuming Ho: µ=70 is true.At a=.05, x-bar values that are less than 67 will lead to the rejection of Ho in favor of Ha: µ < 70The normal curve on the bottom is the sampling distribution for x-bars assuming µ =65.Which area represent the probability of the power of the test?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
C. CExplanation
The area represented by option c represents the probability of the power of the test.Rate this question:
-
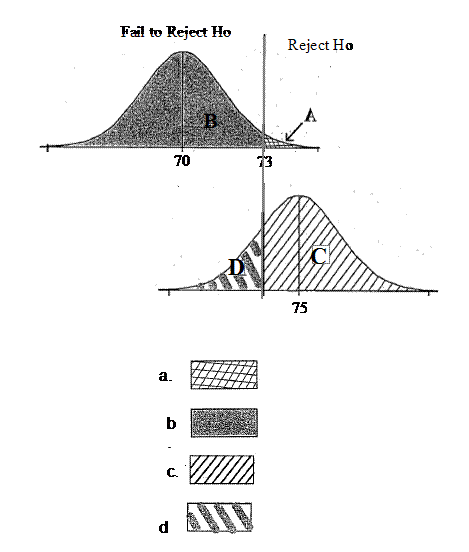
- 10.
Consider the following sampling distributions. The normal curve on the top represents the sampling distribution for x-bars assuming Ho: µ=70 is true.At a=.05, x-bar values that are less than 67 will lead to the rejection of Ho in favor of Ha: µ > 70The normal curve on the bottom is the sampling distribution for x-bars assuming µ =75.Which area represent the probability of Type II error?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
D. DExplanation
The area represented by option d represents the probability of Type II error. Type II error occurs when we fail to reject the null hypothesis (Ho) when it is actually false. In this case, Ho: µ=70 is false, but if we observe a sample mean (x-bar) that falls within the shaded area represented by option d, we would fail to reject Ho and incorrectly conclude that the population mean (µ) is 70. Therefore, option d represents the probability of making a Type II error.Rate this question:
-
- 11.
Consider the following sampling distributions. The normal curve on the top represents the sampling distribution for x-bars assuming Ho: µ=70 is true.At a=.05, x-bar values that are less than 67 will lead to the rejection of Ho in favor of Ha: µ > 70The normal curve on the bottom is the sampling distribution for x-bars assuming µ =75.Which area represent the probability of Type I error?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
A. AExplanation
The area represented by option a represents the probability of Type I error. Type I error occurs when the null hypothesis (Ho) is rejected even though it is true. In this case, the null hypothesis is µ = 70, and if the x-bar values are less than 67, it would lead to the rejection of Ho. Therefore, the area to the left of 67 on the normal curve represents the probability of Type I error.Rate this question:
-
- 12.
Consider the following sampling distributions. The normal curve on the top represents the sampling distribution for x-bars assuming Ho: µ=70At a=.05, x-bar values that are less than 67 will lead to the rejection of Ho in favor of Ha: µ > 70The normal curve on the bottom is the sampling distribution for x-bars assuming µ =75.Which area represent the probability of the power of the test?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
C. CExplanation
The area represented by option c represents the probability of the power of the test. The power of a test is the probability of correctly rejecting the null hypothesis when it is false. In this case, the null hypothesis is that the population mean is 70, and the alternative hypothesis is that the population mean is greater than 70. Option c represents the area under the sampling distribution curve for x-bars assuming a true population mean of 75. This area represents the probability of obtaining a sample mean less than 67, which would lead to correctly rejecting the null hypothesis in favor of the alternative hypothesis.Rate this question:
-
- 13.
We wish to compare two game consoles on the market which were deemed preferred by video game players. Initial testing leads us to believe that Nintendo WII will be more preferred by video game players than Playstation 3. Eighty players are randomly assigned to the two game consoles so that 40 players get WII and 40 players get PS3. The researcher determines in each case whether or not the game console is preferred by video game players. Which statistical procedure should the researcher use for an appropriate test of significance?
- A.
A one sample t-test for means (not matched pairs).
- B.
A two sample t-test for means.
- C.
A matched pairs t-test for means.
- D.
Analysis of Variance (ANOVA)
- E.
A one sample t confidence interval estimate
Correct Answer
B. A two sample t-test for means.Explanation
The researcher wants to compare two game consoles to determine if there is a significant difference in preference among video game players. Since there are two independent groups (WII and PS3) and the researcher wants to compare means (preference), a two sample t-test for means is the appropriate statistical procedure. This test will allow the researcher to determine if there is a significant difference in preference between the two game consoles.Rate this question:
-
- 14.
Researchers want to compare the mean levels of the good cholesterol and in order to do this, they should perform
- A.
A one sample t-test for means (not matched pairs).
- B.
A two sample t-test for means.
- C.
A matched pairs t-test for means.
- D.
Analysis of Variance (ANOVA)
- E.
A one sample t confidence interval estimate
Correct Answer
C. A matched pairs t-test for means.Explanation
In order to compare the mean levels of the good cholesterol, researchers should perform a matched pairs t-test for means. This test is appropriate when the same individuals are measured twice, such as before and after an intervention or treatment. It allows for the comparison of the means between the two time points for the same group of individuals, taking into account the paired nature of the data. This test is suitable for determining if there is a significant difference in the mean levels of the good cholesterol before and after the intervention.Rate this question:
-
- 15.
A random sample of 70 measurements of the free-throw percentage of Jr. Jazz players gave a mean of .60 and standard deviation of .10. Which statistical procedure should be used if we want to estimate the true mean free-throw percentage of the JR Jazz players with 95% confidence?
- A.
A one sample t-test for means (not matched pairs).
- B.
A two sample t-test for means.
- C.
A matched pairs t-test for means.
- D.
Analysis of Variance (ANOVA)
- E.
A one sample t confidence interval estimate
Correct Answer
E. A one sample t confidence interval estimateExplanation
A one sample t confidence interval estimate should be used to estimate the true mean free-throw percentage of the Jr. Jazz players with 95% confidence. This procedure is appropriate when we have a single sample and want to estimate the population mean. The t-test takes into account the sample mean, sample size, and sample standard deviation to calculate a confidence interval that represents the range within which the true population mean is likely to fall. In this case, the mean of .60 and standard deviation of .10 from the random sample of 70 measurements can be used to calculate the confidence interval.Rate this question:
-
- 16.
Students were randomly assigned to each of the three Stats221 classes at BYU Salt Lake Center. Their final scores after the semester were recorded. To see if there are differences between the average Final scores among the three classes, what statistical procedure should be used for the data in this study?
- A.
A one sample t-test for means (not matched pairs).
- B.
A two sample t-test for means.
- C.
A matched pairs t-test for means.
- D.
Analysis of Variance (ANOVA)
- E.
A one sample t confidence interval estimate
Correct Answer
D. Analysis of Variance (ANOVA)Explanation
In this study, the researcher wants to compare the average final scores among the three Stats221 classes. Since there are three independent groups involved, the appropriate statistical procedure to use is Analysis of Variance (ANOVA). ANOVA allows for the comparison of means between multiple groups and determines if there are significant differences among them. The other options, such as one sample t-test or two sample t-test, are not suitable because they are used for comparing means between two groups or a single group, respectively.Rate this question:
-
- 17.
Mangosteen is a fruit containing chemicals called xanthones that are believed to help the body’s cells to function correctly and optimally. In one study four groups of people were compared; the first group was a control group and the other three groups of people were fed either a low dose, a medium dose or a high dose of xanthones from mangosteen. The number of good cells were counted. The following gives the Analysis of Variance (ANOVA) of these data. What can you conclude about the means of the four groups at α=0.05? Assume that the conditions are met for performing this analysis.
- A.
There is no significance difference between the mean count of good cells of the four groups.
- B.
The mean count of good cells is significantly different for all four groups.
- C.
The mean count of good cells of the high dosage group is significantly greater than the mean count of good cells of the control and low dosage.
- D.
On the basis of the P-value, the mean of at least one group differs significantly from the others, but there is no information in the ANOVA outout to determine which mean differs.
Correct Answer
C. The mean count of good cells of the high dosage group is significantly greater than the mean count of good cells of the control and low dosage.Explanation
Based on the given information, the ANOVA analysis suggests that there is a significant difference in the mean count of good cells between the high dosage group and the control and low dosage groups. However, there is no information provided in the ANOVA output to determine if the mean count of good cells is significantly different for all four groups or if there is no significant difference between the mean count of good cells of the four groups. Therefore, the correct answer is that the mean count of good cells of the high dosage group is significantly greater than the mean count of good cells of the control and low dosage groups.Rate this question:
-
- 18.
Mangosteen is a fruit containing chemicals called xanthones that are believed to help the body’s cells to function correctly and optimally. In one study four groups of people were compared; the first group was a control group and the other three groups of people were fed either a low dose, a medium dose or a high dose of xanthones from mangosteen. The number of good cells were counted. The table below gives the Analysis of Variance (ANOVA) of these data.One of the requirements for Analysis of Variances must be equal. On the basis of the output given below, why is that requirement met?Assume that the conditions are met for performing this analysis.
- A.
The P-value for the F test statistic is less than α=0.05.
- B.
The largest standard deviation divided by the smallest standard deviation is less than 2.
- C.
The pooled standard deviation equals 0.4331 which is greater than α=0.05.
- D.
There is no information given in the ANOVA output to determine whether the variances are equal.
Correct Answer
B. The largest standard deviation divided by the smallest standard deviation is less than 2.Explanation
The requirement for equal variances in Analysis of Variance (ANOVA) is met because the largest standard deviation divided by the smallest standard deviation is less than 2. This indicates that the variability among the different groups is relatively similar and there is no significant difference in the spread of the data.Rate this question:
-
- 19.
In practice, if the condition of Normality of the population for t procedures in not met and n < 40, confidence levels and P-values are approximately correct provided:
- A.
α is set very low.
- B.
The sample standard deviation is not large.
- C.
There are no outliers nor strong skewness in the data.
- D.
The data are paired.
Correct Answer
C. There are no outliers nor strong skewness in the data.Explanation
If the condition of Normality of the population for t procedures is not met and n < 40, confidence levels and P-values are approximately correct provided there are no outliers nor strong skewness in the data. This means that even if the population is not normally distributed and the sample size is small, the confidence levels and P-values can still be reliable as long as there are no extreme values or significant asymmetry in the data.Rate this question:
-
- 20.
A study conducted by researchers at BYU investigated the number of months Returned Missionaries get married after coming back from their missions. A random sample of 25 married RM were selected. The average number of months from returning to getting married for these RM’s was 16 months. When testing Ho: µ = 12 months versus Ha: µ > 12 months, the P-value was found to be 0.04. Which of the following is a correct interpretation of this P-value?
- A.
The probability that the mean number of months from returning to getting married by all RM’s was 112 months is 0.04.
- B.
The probability that the mean number of months from returning to getting married by all RM’s does not exceed 12 months is 0.04.
- C.
Only 4% of the RM’s who get married after 12 months or less after their mission; the 96% of the remaining RM’s get married after more than 12 months of returning from missions.
- D.
If the average number of months RM’s get married after their mission was indeed 12 months, the probability that RM’s get married after 16 months or greater is .04.
Correct Answer
D. If the average number of months RM’s get married after their mission was indeed 12 months, the probability that RM’s get married after 16 months or greater is .04.Explanation
The correct interpretation of the P-value is that if the average number of months RM's get married after their mission was indeed 12 months, the probability that RM's get married after 16 months or greater is 0.04.Rate this question:
-
- 21.
The Provo Recreational Office conducted a research of the free-throw percentage of Jr Jazz kids. A percentage of 60% is a “basic” shooting ability and a percentage of 90% is “proficient”. Percentages for a random sample of 1500 Jr Jazz kids from Provo had a mean of 55% with a standard deviation of 20%. What is the value of the standard error of the mean?
- A.
0.0136
- B.
0.1876
- C.
0.5164
- D.
1.8754
- E.
4.5164
Correct Answer
C. 0.5164Explanation
20/sqrt(1500)=.5164Rate this question:
-
- 22.
The average hours spent per week doing the Stats221 homework for BYU students has been 10 hours with a standard deviation of 4 hours. The Statistics Department wanted to test the hypotheses Ho: µ=10 versus Ha: µ<10. They selected an α=0.05 and took a random sample of 100 students who had taken the class. The sample average obtained was 9.75 hours. This result was statistically significant with a P-value <0.01. Are these results also practically significant?
- A.
No, because a 15-minute difference is probably too small to matter.
- B.
No, because the sample is not large enough.
- C.
Yes, because the P-value is less than α
- D.
Yes, because the observed mean is less than 10.
- E.
Yes, because results that are statistically significant are also practically significant.
Correct Answer
A. No, because a 15-minute difference is probably too small to matter.Explanation
The answer "No, because a 15-minute difference is probably too small to matter" is correct because the given information states that the sample average obtained was 9.75 hours, which is only a 15-minute difference from the hypothesized mean of 10 hours. This small difference suggests that there is not a significant practical difference in the amount of time spent on Stats221 homework for BYU students.Rate this question:
-
- 23.
In order to estimate the mean GPA for BYU students, a researcher takes a SRS of GPAs for 81 students. A 96% confidence interval for the mean GPA was computed to be (2.84, 3.06) using x-bar= 2.95 and s=0.5. On the basis of this confidence interval, can we conclude at alpha= 0.04 that the mean GPA for BYU students differs from 3.1?
- A.
No, because 3.1 is within one standard deviation of the sample mean
- B.
No, because the confidence interval does not include the value 3.1.
- C.
Yes, because the BYU students are smarter.
- D.
Yes, because the sample mean of 2.95 is less than 3.1.
- E.
Yes, because the confidence interval does not include the value 3.1.
Correct Answer
E. Yes, because the confidence interval does not include the value 3.1.Explanation
Based on the given information, a 96% confidence interval for the mean GPA was computed to be (2.84, 3.06) using x-bar= 2.95 and s=0.5. The confidence interval does not include the value 3.1, which means that there is evidence to suggest that the mean GPA for BYU students is different from 3.1. Therefore, the correct answer is "Yes, because the confidence interval does not include the value 3.1."Rate this question:
-
- 24.
The life in hours of a particular brand of plasma TV is advertised to have a mean of 30,000 hours. A nationwide electronics chain wants to determine whether to purchase this particular brand. They decide to test a sample of the plasma tvs and purchase these plasma tv unless the test of significance shows evidence that the mean is less 30,000 hours. In other words, they will test the hypotheses ho: µ =30,000 versus Ha: µ < 30,000 and purchase the plasma tv if they fail to reject the null hypotheses. If they reject the null hypothesis, they will not purchase this particular brand of plasma tv. What is the type I error of this test?
- A.
Decide to purchase the plasma tv when the mean life in hours really is 30,000 hours.
- B.
Decide to purchase the plasma tv when the mean life in hours reall is less than 30,000 hours.
- C.
Decide NOT to purchase the plasma tv when the mean life in hours really is 30,000 hours.
- D.
Decide NOT to purchase the plasma tv when the mean life in hours really is less than 30,000 hours.
Correct Answer
C. Decide NOT to purchase the plasma tv when the mean life in hours really is 30,000 hours.Explanation
The type I error of this test is deciding NOT to purchase the plasma TV when the mean life in hours really is 30,000 hours. This means that the electronics chain incorrectly rejects the null hypothesis and concludes that the mean life of the plasma TV is less than 30,000 hours, leading to the decision not to purchase the brand. However, in reality, the mean life is actually 30,000 hours.Rate this question:
-
- 25.
While performing a statistical test of hypotheses, we decide to reject the null hypothesis .What can we say about the Type I and type II errors of our decision?
- A.
We did not make an error because the P-value is small
- B.
We made a type II error, but not a type I error
- C.
We made a type I error, but not a type II error
- D.
We made both a type I and a type II error
Correct Answer
C. We made a type I error, but not a type II errorExplanation
Every time we Reject Ho we can commit a Type I error.
Every time we fail to Reject Ho we can commit a Type II error.Rate this question:
-
- 26.
While performing a statistical test of hypotheses, we decide to fail to reject the null hypothesis. What can we say about the Type I and type II errors of our decision?
- A.
We did not make an error because the P-value is small
- B.
We made a type II error, but not a type I error
- C.
We made a type I error, but not a type II error
- D.
We made both a type I and a type II error
Correct Answer
B. We made a type II error, but not a type I errorExplanation
Every time we Reject Ho we can commit a Type I error.
Every time we fail to Reject Ho we can commit a Type II error.Rate this question:
-
- 27.
An SRS of 500 students in BYU-Provo (population 25,000) responded to a survey which asked their GPA. A 95% confidence interval for the mean GPA was obtained. This survey was also given to a separate SRS of 500 students at the BYU-Salt Lake Center (population 7,000) who also answered the GPA question. A separate 95% confidence interval statement about the mean GPA of all students in the BYU-Slat Lake Center was also constructed. Assume the standard deviation, s, is known and is the same for both groups. The margin of error for the BYU-Salt Lake Center is
- A.
The same as in BYU-Provo, because the two sample sizes are the same.
- B.
Smaller than in BYU-Provo, because the population is much larger in BYU-Provo than BYU-Salt Lake Center.
- C.
Larger than BYU-Provo, because there are fewer students in BYU-Salt Lake
- D.
May be either smaller or larger than BYU-Provo.
Correct Answer
A. The same as in BYU-Provo, because the two sample sizes are the same.Explanation
The margin of error for the BYU-Salt Lake Center is the same as in BYU-Provo because the two sample sizes are the same. The margin of error is influenced by the sample size, with larger sample sizes resulting in smaller margins of error. Since both surveys had a sample size of 500 students, the margin of error would be the same for both groups.Rate this question:
-
- 28.
Coach Sloan suspects that the supplier of the basketball uniforms are sending shirts that easily get torn. He plans to randomly select some shirts from the next batch and perform a test of significance. What can he do to ensure that the power of the test is high?
- A.
Take a small sample of shirts.
- B.
Take a large sample of shirts.
- C.
Wear each one of them.
- D.
Let the other team wear them.
Correct Answer
B. Take a large sample of shirts.Explanation
To ensure that the power of the test is high, Coach Sloan should take a large sample of shirts. By increasing the sample size, he will have a better chance of detecting any significant differences in the quality of the shirts. A larger sample size reduces the likelihood of random variation and increases the precision of the test, making it more likely to detect any true differences in the quality of the shirts.Rate this question:
-
- 29.
A study was conducted to determine the average GPA of students enrolled at the BYU Salt Lake Center. A random sample of 50 students was selected, the mean GPA computed and a 90% confidence interval obtained. The resulting confidence interval is (2.35, 3.87). This interval gives us
- A.
The range of reasonable values for the true mean GPA of students enrolled at the BYU Salt Lake Center.
- B.
The range of reasonable values for the sample mean GPA of students enrolled at the BYU Salt Lake Center.
- C.
The range of reasonable values for the true standard deviation of GPA of students enrolled at the BYU Salt Lake Center.
- D.
The range for 90% of GPA’s of all students enrolled at the BYU Salt Lake Center.
Correct Answer
A. The range of reasonable values for the true mean GPA of students enrolled at the BYU Salt Lake Center.Explanation
The confidence interval (2.35, 3.87) provides a range of reasonable values for the true mean GPA of students enrolled at the BYU Salt Lake Center. This means that we can be 90% confident that the true mean GPA falls within this interval.Rate this question:
-
- 30.
Suppose that a researcher would like to predict the results of mayoral election on 20 cities in Utah. We randomly poll 1501 voters from all these cities. For each city he either “called” a winner or declared the election “too close to call.” The researcher correctly predicted the outcome of 19 elections. However, for one of the mayoral election, the researcher “called Anderson the winner when Sotomayor actually won the election. What is the most likely explanation for this mistake?
- A.
The researcher is biased against minorities.
- B.
The researcher does not like Sotomayor.
- C.
Multiple analyses increase the chances of making a Type I error.
- D.
Multiple analyses increase the chances of making a Type II error.
Correct Answer
C. Multiple analyses increase the chances of making a Type I error.Explanation
The most likely explanation for the researcher's mistake is that multiple analyses increase the chances of making a Type I error. This means that with multiple predictions, there is a higher probability of incorrectly predicting the outcome of an election. In this case, the researcher correctly predicted the outcome of 19 elections, but made an error in one. This suggests that the mistake was likely due to the increased likelihood of making a Type I error when analyzing multiple elections.Rate this question:
-
- 31.
Which one of the following situations will best allow a cause-and-effect conclusion about the relationship between smoking and lung cancer?
- A.
Take a random sample of 100 mean, ask them who smoke and who does not. Record the incidence of lung cancer between those who smoke and those who do not.
- B.
Ask for volunteer of 100 mean, ask them who smoke and who does not. Record the incidence of lung cancer between those who smoke and those who do not.
- C.
Take a random sample of 100 men. Randomly assign them into two groups. Ask the first group to smoke for 10 years and the other group not to smoke. After 10 years measure the incidence of lung cancer between the two groups using a two sample t-test.
- D.
Randomly ask 100 lawyers whether smoking causes cancer.
Correct Answer
C. Take a random sample of 100 men. Randomly assign them into two groups. Ask the first group to smoke for 10 years and the other group not to smoke. After 10 years measure the incidence of lung cancer between the two groups using a two sample t-test.Explanation
The best situation that allows a cause-and-effect conclusion about the relationship between smoking and lung cancer is to take a random sample of 100 men and randomly assign them into two groups. One group should be asked to smoke for 10 years while the other group should not smoke. After 10 years, the incidence of lung cancer between the two groups should be measured using a two sample t-test. This controlled experiment allows for the comparison of lung cancer rates between smokers and non-smokers, providing evidence for a cause-and-effect relationship.Rate this question:
-
- 32.
A study was conducted using growing rats to examine the effect of jumping height on the strength of bones. Thirty rats were randomly allocated into groups. The first group of rats did low jumps of 30 cm. And the second group of rats did high jumps of 60 cm. After 8 weeks of 10 jumps per day, 5 days per week, the bone density of the rats was measured in mg/cm3. What is the response variable?
- A.
Growing rats
- B.
Height of jump
- C.
Bone density as measured in mg/cm3.
- D.
Age of rat
Correct Answer
C. Bone density as measured in mg/cm3.Explanation
The response variable in this study is the bone density of the rats, which is measured in mg/cm3. The study aims to examine the effect of jumping height on the strength of bones, and bone density is a measure of bone strength. By comparing the bone density of rats that did low jumps of 30 cm with those that did high jumps of 60 cm, the researchers can determine if jumping height has an impact on bone density.Rate this question:
-
- 33.
The following hypotheses were tested: Ho: µ=75 versus Ha: µ > 75 where µ is the true mean score for Stats221 finals. The test scores of a random sample of students who have taken Stats221 had a mean x-bar = 78. The hypothesis test produced a P-value of 0.314. With alpha=0.05, do the data give sufficient evidence that the mean final score is greater than 75?
- A.
No, because the p-value is not less than alpha
- B.
No, because the results are statistical significant.
- C.
No, because the p-value is less than alpha.
- D.
Yes, because the p-value is not less than alpha.
- E.
Yes, because the p-value is less than alpha.
Correct Answer
A. No, because the p-value is not less than alphaExplanation
The correct answer is "No, because the p-value is not less than alpha." This means that the data does not provide sufficient evidence to reject the null hypothesis. The p-value is the probability of obtaining a test statistic as extreme as the one observed, assuming the null hypothesis is true. In this case, the p-value is greater than the significance level (alpha=0.05), indicating that the observed mean score of 78 is not significantly different from the hypothesized mean score of 75.Rate this question:
-
- 34.
The following hypotheses were tested: Ho: µ=75 versus Ha: µ > 75 where µ is the true mean score for Stats221 finals. The test scores of a random sample of students who have taken Stats221 had a mean x-bar = 78. The hypothesis test produced a P-value of 0.0314. With alpha=0.05, do the data give sufficient evidence that the mean final score is greater than 75?0
- A.
No, because the p-value is not less than alpha
- B.
No, because the results are statistical significant.
- C.
No, because the p-value is less than alpha.
- D.
Yes, because the p-value is not less than alpha.
- E.
Yes, because the p-value is less than alpha.
Correct Answer
E. Yes, because the p-value is less than alpha.Explanation
The correct answer is "Yes, because the p-value is less than alpha." In hypothesis testing, the p-value represents the probability of obtaining a test statistic as extreme as the one observed, assuming the null hypothesis is true. In this case, the p-value is 0.0314, which is less than the significance level alpha of 0.05. This means that there is sufficient evidence to reject the null hypothesis and conclude that the mean final score is greater than 75.Rate this question:
-
- 35.
Which one of the following statements best describes the logic of tests of significance?
- A.
An outcome that is quite likely to happen if Ho were true is good evidence that Ho is true.
- B.
If the probability of Ho being true is very small, then Ho cannot be true.
- C.
If the probability of an outcome occurring is quite likely, then the claim as stated in Ho about the outcome must be correct.
- D.
An outcome that would rarely happen if Ho were true is good evidence that Ho is not true.
Correct Answer
D. An outcome that would rarely happen if Ho were true is good evidence that Ho is not true.Explanation
The correct answer suggests that if an outcome is unlikely to occur if the null hypothesis (Ho) is true, then it is strong evidence that the null hypothesis is not true. This is because if the null hypothesis were true, the outcome would be expected to happen more frequently. Therefore, the occurrence of a rare outcome contradicts the null hypothesis and supports an alternative hypothesis.Rate this question:
-
- 36.
For a one sided test on µ with σ known, the P-value is represented as the area in the tail of a Normal curve. What does this Normal curve represent?
- A.
Values of the measurements in the sample data set.
- B.
All possible measurements for the response variable and their frequencies.
- C.
The population of measurements about which we wish to make an inference.
- D.
All possible values of x-bars and how often they occur if Ho were true.
Correct Answer
D. All possible values of x-bars and how often they occur if Ho were true.Explanation
The Normal curve represents all possible values of x-bars and how often they occur if the null hypothesis (Ho) were true. This means that the curve represents the distribution of sample means that would be obtained if the null hypothesis were true. The area in the tail of the Normal curve represents the probability of observing a sample mean as extreme as the one obtained in the actual data, assuming that the null hypothesis is true.Rate this question:
-
- 37.
GPA of students of a specified population are Normally distributed with known standard deviation of 1.1 points. A 95% confidence interval, (2.35, 3.87), was calculated from a simple random sample of twenty-five students. Which of the following is a correct interpretation of “95% confidence”?
- A.
If this study were to be repeated a large number of times, approximately 95% of the confidence interval would include the true mean.
- B.
95% of the students’ GPA in the population are contained in the confidence interval.
- C.
The interval contains 95% of the sample GPAs.
- D.
If this study were to be repeated a large number of times, 95% of the sample means would be included in this particular confidence interval: (2.35, 3.87).
Correct Answer
A. If this study were to be repeated a large number of times, approximately 95% of the confidence interval would include the true mean.Explanation
The correct interpretation of "95% confidence" is that if this study were to be repeated a large number of times, approximately 95% of the confidence intervals calculated would include the true mean GPA of the population. This means that there is a high level of confidence that the true mean falls within the given interval.Rate this question:
-
- 38.
The significance level is set at α=.05 and a hypothesis test results in a P-value of .02. Which one of the following is a correct conclusion based on the P-value?
- A.
The data are consistent with the null hypothesis. Therefore, we do not reject the null hypothesis.
- B.
The data are consistent with the null hypothesis. Therefore, we reject the null hypothesis.
- C.
The data are not consistent with the null hypothesis. Therefore, we do not reject the null hypothesis.
- D.
The data are not consistent with the null hypothesis. Therefore, we reject the null hypothesis.
- E.
There is a 2% chance that the null hypothesis is true. Therefore, we reject the null hypothesis.
Correct Answer
D. The data are not consistent with the null hypothesis. Therefore, we reject the null hypothesis.Explanation
The correct conclusion based on the P-value of .02 is that the data are not consistent with the null hypothesis. Therefore, we reject the null hypothesis. This is because the P-value is less than the significance level of α=.05, indicating that the probability of obtaining the observed data under the assumption that the null hypothesis is true is very low. Thus, we have evidence to reject the null hypothesis and support an alternative hypothesis.Rate this question:
-
- 39.
The significance level is set at α=.01 and a hypothesis test results in a P-value of .02. Which one of the following is a correct conclusion based on the P-value?
- A.
The data are consistent with the null hypothesis. Therefore, we do not reject the null hypothesis.
- B.
The data are consistent with the null hypothesis. Therefore, we reject the null hypothesis.
- C.
The data are not consistent with the null hypothesis. Therefore, we reject the null hypothesis.
- D.
There is a 2% chance that the null hypothesis is true. Therefore, we reject the null hypothesis.
- E.
There is a 2% chance that the alternative hypothesis is true. Therefore, we accept the null hypothesis.
Correct Answer
A. The data are consistent with the null hypothesis. Therefore, we do not reject the null hypothesis.Explanation
The correct conclusion based on the P-value of .02 is that the data are consistent with the null hypothesis. This means that there is not enough evidence to reject the null hypothesis at the significance level of α=.01.Rate this question:
-
- 40.
Based on a random sample of 50 students and a known population and sigma, a 90% confidence interval for the mean GPA of all students was calculated as (2.35, 3.87). Which of the following is a correct statement regarding this confidence interval?
- A.
90% of the GPA of students are between (2.35, 3.87).
- B.
90% of the time, the mean GPA of students will be in the interval from 2.35 to 3.87.
- C.
We are 90% confident that the mean GPA of students is between 2.35 and 3.87.
- D.
We are 90% confident that the interval (2.35, 3.87) contains the mean GPA of this sample of 50 students.
Correct Answer
C. We are 90% confident that the mean GPA of students is between 2.35 and 3.87.Explanation
The correct answer is "We are 90% confident that the mean GPA of students is between 2.35 and 3.87." This statement accurately reflects the interpretation of a confidence interval. A confidence interval provides a range of values within which the true population parameter is likely to fall, with a specified level of confidence. In this case, the confidence interval suggests that we can be 90% confident that the mean GPA of all students falls between 2.35 and 3.87.Rate this question:
-
- 41.
In addition to having an SRS, what should be checked in order to validly use the formula when n=15?
- A.
No other checks necessary.
- B.
Whether the plot of the population is approximately Normal.
- C.
No pattern in the residual plot.
- D.
No outliers or strong skewness in a plot of the data.
Correct Answer
D. No outliers or strong skewness in a plot of the data.Explanation
To validly use the formula when n=15, it is important to check for outliers or strong skewness in a plot of the data. This is because outliers or strong skewness can significantly affect the validity of the formula and the accuracy of the results. Therefore, it is necessary to ensure that the data does not contain any extreme values or unusual distributions that could impact the analysis.Rate this question:
-
- 42.
A SRS of 64 BYU students found that the average GPA was x-bar=2.7. Assuming the population standard deviation is known to be 0.3, a margin of error for a 95% confidence interval for the population average GPA is calculated to be 0.0735. Which action below would result in a smaller margin of error?
- A.
Using a confidence level of 99%
- B.
Using a sample of 50 students.
- C.
Using a sample of 100 students.
- D.
Taking a different sample of 64 students.
Correct Answer
C. Using a sample of 100 students.Explanation
Using a sample of 100 students would result in a smaller margin of error because a larger sample size leads to a more accurate estimate of the population parameter. As the sample size increases, the variability decreases, resulting in a smaller margin of error.Rate this question:
-
- 43.
A SRS of 64 BYU students found that the average GPA was x-bar=2.7. Assuming the population standard deviation is known to be 0.3, a margin of error for a 95% confidence interval for the population average GPA is calculated to be 0.0735. Which action below would result in a larger margin of error?
- A.
Using a confidence level of 99%.
- B.
Using a confidence level of 90%
- C.
Using a sample of 100 students
- D.
Taking a different sample of 64 students.
Correct Answer
A. Using a confidence level of 99%.Explanation
Using a confidence level of 99% would result in a larger margin of error because a higher confidence level requires a wider interval to capture a larger range of possible values. This means that there is a higher level of certainty in the estimate, but it also leads to a larger margin of error.Rate this question:
-
- 44.
Researchers have postulated that because of differences in teachers, students at the BYU Salt Lake Center should have a higher GPA than BYU-Provo students. Suppose the mean GPA of BYU-Provo students is known to be 3.2. What hypothesis are being tested?
- A.
Ho: µ = 3.2 and Ha: µ > 3.2
- B.
Ho: µ = 3.2 and Ha: µ < 3.2
- C.
Ho: µ = 3.2 and Ha: µ ≠ 3.2
- D.
Ho: x ̅ =3.2 and Ho: x ̅ >3.2
Correct Answer
A. Ho: µ = 3.2 and Ha: µ > 3.2Explanation
The hypothesis being tested is that the mean GPA of BYU-Provo students is equal to 3.2 (Ho: µ = 3.2) and the alternative hypothesis is that the mean GPA of BYU-Provo students is greater than 3.2 (Ha: µ > 3.2). This suggests that the researchers are interested in determining if there is a significant difference in GPA between BYU-Provo students and BYU Salt Lake Center students, with the expectation that the BYU Salt Lake Center students have a higher GPA.Rate this question:
-
- 45.
Researchers have postulated that there is no differences in GPA of the BYU Salt Lake Center and BYU-Provo students. Suppose the mean GPA of BYU-Provo students is known to be 3.2. What hypothesis are being tested?
- A.
Ho: µ = 3.2 and Ha: µ > 3.2
- B.
Ho: µ = 3.2 and Ha: µ < 3.2
- C.
Ho: µ = 3.2 and Ha: µ ≠ 3.2
- D.
Ho: x ̅ =3.2 and Ho: x ̅ ≠ 3.2
Correct Answer
C. Ho: µ = 3.2 and Ha: µ ≠ 3.2Explanation
The hypothesis being tested is Ho: µ = 3.2 and Ha: µ ≠ 3.2. This hypothesis suggests that there is no difference in the mean GPA of BYU Salt Lake Center and BYU-Provo students, with the null hypothesis stating that the mean GPA is equal to 3.2 and the alternative hypothesis stating that the mean GPA is not equal to 3.2.Rate this question:
-
- 46.
Which of the following questions does a test of significance answer?
- A.
Is the sample or experiment properly designed?
- B.
Is the observed effect too large to be due to chance alone?
- C.
How much confidence can be placed in the observed effect?
- D.
What is the probability that the parameter is different from the statistic?
Correct Answer
B. Is the observed effect too large to be due to chance alone?Explanation
A test of significance answers the question of whether the observed effect is too large to be due to chance alone. It determines the probability of obtaining the observed result if there is no real effect or difference. If the probability is very low (typically below a predetermined significance level), it suggests that the observed effect is unlikely to be due to chance and is therefore considered statistically significant.Rate this question:
-
- 47.
Suppose we want a 95% confidence interval for the average amount spend on dates at BYU. The amount spend on dates follow a normal distribution with a standard deviation σ= $20. How large should the sample be so that 95% confidence interval has a margin of error of $3?
- A.
170
- B.
170.7
- C.
171
- D.
100
Correct Answer
C. 171Explanation
To calculate the sample size needed for a 95% confidence interval with a margin of error of $3, we need to use the formula for sample size calculation. The formula is:
n = (Z * σ / E)^2
Where:
n = sample size
Z = Z-score for the desired confidence level (for 95% confidence level, Z = 1.96)
σ = standard deviation
E = margin of error
Plugging in the values, we have:
n = (1.96 * 20 / 3)^2
n = (39.2 / 3)^2
n = 13.07^2
n ≈ 170.7
Therefore, the sample size needed for a 95% confidence interval with a margin of error of $3 is approximately 171.Rate this question:
-
- 48.
When performing a one-sample t-test of Ho: µ=µo versus Ha: µ>µo, the observed effect is equal to the difference between x-bar and µo (i.e.,x-bar - µo). For a fixed sample size, if the observed effect were to increase, what would happen to the P-value?
- A.
It would get smaller.
- B.
It would stay the same.
- C.
It would get bigger.
Correct Answer
A. It would get smaller.Explanation
When performing a one-sample t-test, the P-value represents the probability of obtaining a test statistic as extreme as the observed effect, assuming the null hypothesis is true. As the observed effect increases, the test statistic becomes more extreme, resulting in a smaller P-value. Therefore, if the observed effect were to increase, the P-value would get smaller.Rate this question:
-
- 49.
When performing a one-sample t-test of Ho: µ=µo versus Ha: µ>µo, the observed effect is equal to the difference between x-bar and µo (i.e.,x-bar - µo). For a fixed sample size, if the observed effect were to decrease, what would happen to the P-value?
- A.
It would get smaller.
- B.
It would stay the same.
- C.
It would get bigger.
Correct Answer
C. It would get bigger.Explanation
If the observed effect were to decrease, it means that the difference between x-bar and µo becomes smaller. This would result in a smaller t-value and a larger p-value. A larger p-value indicates that the observed effect is more likely to occur by chance, therefore the null hypothesis (Ho) is more likely to be true. Therefore, the correct answer is that the p-value would get bigger.Rate this question:
-
- 50.
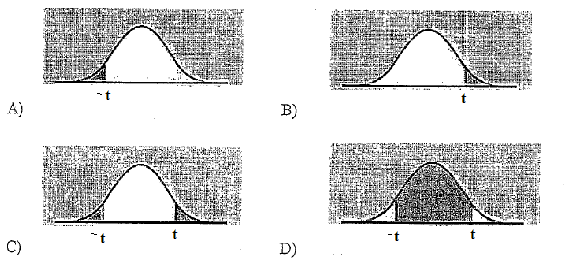
The mean percentage free-throw of 12th graders is 65%. A researcher suspects that varsity players have higher free-throw percentages than 12th graders in general. He conduct a study using Ho: µ=65% vs. Ha: µ>65% and computes t-test statistic of 1.5. Which of the following graphs show the appropriate shaded area for the P-value of this test?
- A.
A
- B.
B
- C.
C
- D.
D
Correct Answer
B. BExplanation
The t-test statistic of 1.5 indicates that the sample mean is 1.5 standard deviations above the population mean. The alternative hypothesis (Ha: µ>65%) suggests that the researcher is looking for a right-tailed test. Therefore, the appropriate shaded area for the p-value would be on the right side of the distribution curve. Graph b correctly shows the shaded area on the right side, indicating the p-value for the test.Rate this question:
-
Quiz Review Timeline +
Our quizzes are rigorously reviewed, monitored and continuously updated by our expert board to maintain accuracy, relevance, and timeliness.
-
Current Version
-
Mar 21, 2023Quiz Edited by
ProProfs Editorial Team -
May 31, 2009Quiz Created by
Doriarg
 Back to top
Back to top